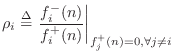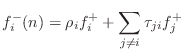The reflection coefficient seen at port  is defined as
is defined as
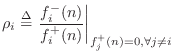 |
(F.20) |
In other words, the
reflection coefficient specifies what portion of
the incoming wave

is
reflected back to port

as
part of the outgoing wave
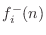
. The total outgoing wave on port

is the
superposition of the reflected wave and the
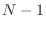
transmitted waves from the other ports:
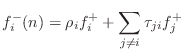 |
(F.21) |
where
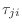
denotes the
transmission coefficient from
port

to port

. Starting with Eq.

(
F.19) and substituting
Eq.

(
F.18) gives
Equating like terms with Eq. (F.21), we obtain
(F.21), we obtain
Thus, the

th alpha parameter is the
force transmission coefficient
from

th port to any other port (besides the

th). To convert the
transmission coefficient from the

th port to the reflection
coefficient for that port, we simply subtract 1. This general
relationship is specific to
force waves at a parallel junction, as we
will soon see.
Next Section: Physical Derivation of Reflection CoefficientPrevious Section: Alpha Parameters
![]() is defined as
is defined as
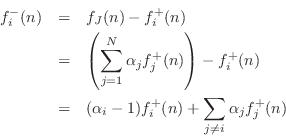
![]() (F.21), we obtain
(F.21), we obtain