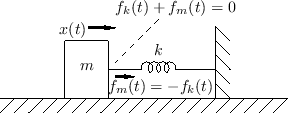Applying Newton's Laws of Motion
As a simple example, consider a mass  driven along a frictionless
surface by an ideal spring
driven along a frictionless
surface by an ideal spring  , as shown in Fig.B.2.
Assume that the mass position
, as shown in Fig.B.2.
Assume that the mass position  corresponds to the spring at rest,
i.e., not stretched or compressed. The force necessary to compress the
spring by a distance
corresponds to the spring at rest,
i.e., not stretched or compressed. The force necessary to compress the
spring by a distance  is given by Hooke's law (§B.1.3):
is given by Hooke's law (§B.1.3):
This force is balanced at all times by the
inertial force
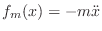
of
the mass

,
i.e. 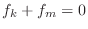
,
yielding
B.6
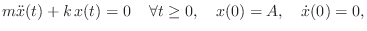 |
(B.4) |
where we have defined

as the initial
displacement of the mass
along

. This is a
differential equation whose solution
gives the equation of motion of the mass-spring junction for all
time:
B.7
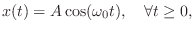 |
(B.5) |
where
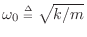
denotes the
frequency of
oscillation in radians per second. More generally, the complete
space of solutions to Eq.

(
B.4), corresponding to all possible
initial displacements

and initial velocities
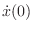
, is the
set of all
sinusoidal oscillations at frequency
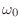
:
The amplitude of oscillation

and phase offset
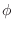
are
determined by the
initial conditions,
i.e., the initial position

and initial
velocity
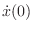
of the mass (its
initial
state) when we ``let it go'' or ``push it off'' at time
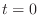
.
Next Section: Potential Energy
in a SpringPrevious Section: Hooke's Law
![]() driven along a frictionless
surface by an ideal spring
driven along a frictionless
surface by an ideal spring ![]() , as shown in Fig.B.2.
Assume that the mass position
, as shown in Fig.B.2.
Assume that the mass position ![]() corresponds to the spring at rest,
i.e., not stretched or compressed. The force necessary to compress the
spring by a distance
corresponds to the spring at rest,
i.e., not stretched or compressed. The force necessary to compress the
spring by a distance ![]() is given by Hooke's law (§B.1.3):
is given by Hooke's law (§B.1.3):