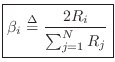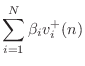Beta Parameters
It is customary in the wave digital filter literature to define the beta parameters as
where
However, we normally employ a mixture of parallel and series adaptors,
while keeping a force-wave simulation. Since
![]() , we obtain, after a small amount of algebra, the following
recipe for the series force-wave adaptor:
, we obtain, after a small amount of algebra, the following
recipe for the series force-wave adaptor:
We see that we have
Next Section:
Reflection Coefficient, Series Case
Previous Section:
Reflection Free Port