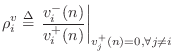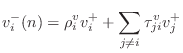The velocity reflection coefficient seen at port
 is defined as
is defined as
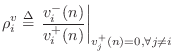 |
(F.31) |
Representing the outgoing velocity wave
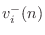
as the
superposition of the reflected wave
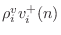
plus the
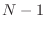
transmitted waves from the other ports, we have
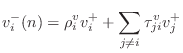 |
(F.32) |
where

denotes the
velocity transmission
coefficientvelocity!transmission
coefficient from
port

to port

. Substituting Eq.

(
F.29) into
Eq.

(
F.30) yields
Equating like terms with Eq. (F.32) gives
(F.32) gives
Thus, the

th beta parameter is the velocity transmission
coefficient from

th port to any other port (besides the

th). To
convert the transmission coefficient from the

th port to the
reflection coefficient for that port, we simply subtract 1. These
relationships are specific to velocity waves at a series junction
(cf. Eq.

(
F.22)). They are exactly the dual of Equations (
F.22-
F.23)
for
force waves at a parallel junction.
Next Section: Physical Derivation of Series Reflection CoefficientPrevious Section: Beta Parameters
![]() is defined as
is defined as
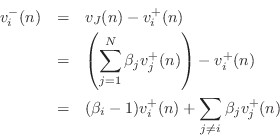
![]() (F.32) gives
(F.32) gives