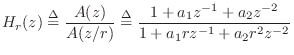Body Factoring Example
![\includegraphics[width=3.5in]{eps/fbrBodyIRandShortenedmatti}](http://www.dsprelated.com/josimages_new/pasp/img1874.png) |
Figure 8.14a shows the impulse
response of a classical guitar body sampled at ![]() kHz. It was
determined empirically that at least the first
kHz. It was
determined empirically that at least the first ![]() msec of this
impulse response needs to be stored in the excitation table to produce
a high quality synthetic guitar. Figure
8.14b shows the same impulse response
after factoring out a single resonating mode near
msec of this
impulse response needs to be stored in the excitation table to produce
a high quality synthetic guitar. Figure
8.14b shows the same impulse response
after factoring out a single resonating mode near ![]() Hz (the main
Helmholtz air mode). A close-up of the initial response is shown in
Fig. 8.15. As can be seen, the
residual response is considerably shorter than the original.
Hz (the main
Helmholtz air mode). A close-up of the initial response is shown in
Fig. 8.15. As can be seen, the
residual response is considerably shorter than the original.
![\includegraphics[width=3.5in]{eps/fbrBodyFRandShortenedmatti}](http://www.dsprelated.com/josimages_new/pasp/img1877.png) |
Figure 8.16a shows the guitar-body amplitude response, and Fig. 8.16b shows the response after the main Helmholtz air mode is removed by inverse filtering with a two-pole, two-zero filter. Figure 8.18 shows the same thing but with only a two-zero inverse filter; in this case the overall spectral shape is more affected.
![\includegraphics[width=3.5in]{eps/fbrBodyFRandShortenedmattiRat0}](http://www.dsprelated.com/josimages_new/pasp/img1879.png) |
![\includegraphics[width=3.5in]{eps/fbrBodyFRandShortenedmattiw}](http://www.dsprelated.com/josimages_new/pasp/img1880.png) |
![\includegraphics[width=3.5in]{eps/fbrBodyFRandShortenedmattiwRat0}](http://www.dsprelated.com/josimages_new/pasp/img1882.png) |
Figure 8.19a shows the measured guitar-body amplitude response after warping to an approximate Bark frequency axis. Figure 8.19b shows the Bark-warped amplitude response after the main Helmholtz air mode is removed by inverse filtering. Fig. 8.20 shows the low-frequency close-up. The warped amplitude response was computed as the FFT of the impulse response of the FIR filter given by the original impulse response with each unit delay being replaced by a first-order allpass filter, as originally suggested in [334] and described further in [229].
Fig. 8.21 shows the corresponding
results if a two-zero inverse filter is used rather than a two-pole,
two-zero inverse filter, i.e., without the ``isolation poles,'' (![]() in Eq.
in Eq.![]() (8.18) below). In this case, there is an overall ``EQ''
boosting high frequencies and attenuating low frequencies. However,
comparing Figs. 8.18b and
8.21b, we see that the global EQ
effect is less pronounced in the Bark-warped case. On the Bark
frequency scale, it is much easier numerically to eliminate the main
air mode.
(8.18) below). In this case, there is an overall ``EQ''
boosting high frequencies and attenuating low frequencies. However,
comparing Figs. 8.18b and
8.21b, we see that the global EQ
effect is less pronounced in the Bark-warped case. On the Bark
frequency scale, it is much easier numerically to eliminate the main
air mode.
The modal bandwidth used in the inverse filtering was chosen to be
![]() Hz which corresponds to a
Hz which corresponds to a ![]() of
of ![]() for the main air mode. If
the Bark-warping is done using a first-order conformal map
[458], its inverse preserves filter order
[428, pp. 61-67]. Applying the inverse warping to the
parametric resonator drives its pole radius from
for the main air mode. If
the Bark-warping is done using a first-order conformal map
[458], its inverse preserves filter order
[428, pp. 61-67]. Applying the inverse warping to the
parametric resonator drives its pole radius from ![]() in the
Bark-warped
in the
Bark-warped ![]() plane to
plane to ![]() in the unwarped
in the unwarped ![]() plane.
plane.
Note that if the inverse filter consists only of two zeros determined by the spectral peak parameters, other portions of the spectrum will be modified by the inverse filtering, especially at the next higher resonance, and in the linear trend of the overall spectral shape. To obtain a more localized mode extraction (useful when the procedure is to be repeated), we define the inverse filter as
where
Because the main air mode is extremely narrow, the probability of overflow
can be reduced in fixed-point implementations by artificially dampening it.
Reducing the ![]() of the main Helmholtz air mode from
of the main Helmholtz air mode from ![]() to
to ![]() corresponds to a decay time of about
corresponds to a decay time of about
![]() sec.
This is consistent with the original desire to retain the first
sec.
This is consistent with the original desire to retain the first ![]() msec
of the body impulse response.
msec
of the body impulse response.
![\includegraphics[width=\twidth]{eps/fbrBodyIRandShortenedmattiw}](http://www.dsprelated.com/josimages_new/pasp/img1889.png) |
For completeness, the Bark-warped impulse-responses are also shown in Figs. 8.22. Figure 8.22a shows the complete Bark-warped impulse response obtained by taking the inverse FFT of Fig. 8.19a, and Fig. 8.22b shows the shortened Bark-warped impulse response defined as the inverse FFT of Fig. 8.19b. We see that given a Bark-warped frequency axis (which more accurately represents what we hear), the time duration of the high-frequency modes is extended while the low-frequency modes are contracted in time duration. Thus, the modal decay times show less of a spread versus frequency. This also accounts for the reduced apparent shortening by the inverse filtering in the Bark-warped case.
Next Section:
Phasing with First-Order Allpass Filters
Previous Section:
Approximating Shortened Excitations as Noise








![\includegraphics[width=3.5in]{eps/fbrZoomedBodyIRandShortenedmatti}](http://www.dsprelated.com/josimages_new/pasp/img1875.png)
![\includegraphics[width=3.5in]{eps/fbrZoomedBodyFRandShortenedmatti}](http://www.dsprelated.com/josimages_new/pasp/img1878.png)
![\includegraphics[width=3.5in]{eps/fbrZoomedBodyFRandShortenedmattiw}](http://www.dsprelated.com/josimages_new/pasp/img1881.png)