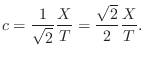Free Books
   Free Books    Physical Audio Signal Processing  

2D Mesh and the Wave Equation

Figure C.33: Region of nodes in a rectilinear waveguide mesh.
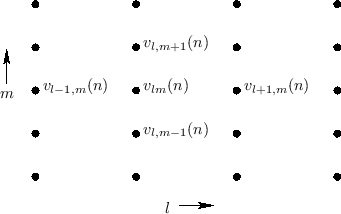
\includegraphics{eps/mesh}

Figure C.34: Zoom-in about node $ (l,m)$ at time $ n$ in a rectilinear waveguide mesh, showing traveling-wave components entering and leaving the node. (All variables are at time $ n$,)
\includegraphics{eps/meshzoom}
Consider the 2D rectilinear mesh, with nodes at positions $ x=lX$ and $ y=mY$, where $ l$ and $ m$ are integers, and $ X$ and $ Y$ denote the spatial sampling intervals along $ x$ and $ y$, respectively (see Fig.C.33). Then from Eq.$ \,$(C.105) the junction velocity $ v_{lm}$ at time $ n$ is given by

$\displaystyle v_{lm}(n) = \frac{1}{2}\left[ v_{lm}^{+\textsc{n}}(n) + v_{lm}^{+\textsc{e}}(n) + v_{lm}^{+\textsc{s}}(n) + v_{lm}^{+\textsc{w}}(n)\right] $

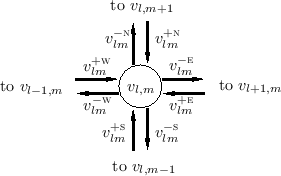
where $ v_{lm}^{+\textsc{n}}(n)$ is the ``incoming wave from the north'' to node $ (l,m)$, and similarly for the waves coming from east, west, and south (see Fig.C.34). These incoming traveling-wave components arrive from the four neighboring nodes after a one-sample propagation delay. For example, $ v_{lm}^{+\textsc{n}}(n)$, arriving from the north, departed from node $ (l,m+1)$ at time $ n-1$, as $ v_{l,m+1}^{-\textsc{s}}(n-1)$. Furthermore, the outgoing components at time $ n$ will arrive at the neighboring nodes one sample in the future at time $ n+1$. For example, $ v_{lm}^{-\textsc{n}}(n)$ will become $ v_{l,m+1}^{+\textsc{s}}(n+1)$. Using these relations, we can write $ v_{lm}(n+1)$ in terms of the four outgoing waves from its neighbors at time $ n$:

$\displaystyle v_{lm}(n+1) = \frac{1}{2}\left[ v_{l,m+1}^{-\textsc{s}}(n) + v_{l... ...}}(n) + v_{l,m-1}^{-\textsc{n}}(n) + v_{l-1,m}^{-\textsc{e}}(n)\right] \protect$ (C.116)

where, for instance, $ v_{lm}^{-\textsc{n}}(n)$ is the ``outgoing wave to the north'' from node $ (l,m)$. Similarly, the outgoing waves leaving $ v_{lm}(n-1)$ become the incoming traveling-wave components of its neighbors at time $ n$:

$\displaystyle v_{lm}(n-1) = \frac{1}{2}\left[ v_{l,m+1}^{+\textsc{s}}(n) + v_{l... ...}}(n) + v_{l,m-1}^{+\textsc{n}}(n) + v_{l-1,m}^{+\textsc{e}}(n)\right] \protect$ (C.117)

This may be shown in detail by writing
\begin{eqnarray*} v_{lm}(n-1) &=& \frac{1}{2}[v_{lm}^{+\textsc{n}}(n-1) + \cdot... ...}^{-\textsc{n}}(n-1) + \cdots + v_{lm}^{-\textsc{w}}(n-1)\right] \end{eqnarray*}
so that
\begin{eqnarray*} v_{lm}(n-1) &=& \frac{1}{2}[v_{lm}^{-\textsc{n}}(n-1) + \cdot... ... v_{l,m-1}^{+\textsc{n}}(n) + v_{l-1,m}^{+\textsc{e}}(n)\right]. \end{eqnarray*}
Adding Equations (C.116-C.116), replacing terms such as $ v_{l,m+1}^{+\textsc{s}}(n) + v_{l,m+1}^{-\textsc{s}}(n)$ with $ v_{l,m+1}(n)$, yields a computation in terms of physical node velocities:
\begin{eqnarray*} \lefteqn{v_{lm}(n+1) + v_{lm}(n-1) = } \\ & & \frac{1}{2}\left[ v_{l,m+1}(n) + v_{l+1,m}(n) + v_{l,m-1}(n) + v_{l-1,m}(n)\right] \end{eqnarray*}
Thus, the rectangular waveguide mesh satisfies this equation giving a formula for the velocity at node $ (l,m)$, in terms of the velocity at its neighboring nodes one sample earlier, and itself two samples earlier. Subtracting $ 2v_{lm}(n)$ from both sides yields
\begin{eqnarray*} \lefteqn{v_{lm}(n+1) - 2 v_{lm}(n) + v_{lm}(n-1)} \\ &=& \fra... .... \left[v_{l+1,m}(n) - 2 v_{lm}(n) + v_{l-1,m}(n)\right]\right\} \end{eqnarray*}
Dividing by the respective sampling intervals, and assuming $ X=Y$ (square mesh-holes), we obtain
\begin{eqnarray*} \lefteqn{\frac{v_{lm}(n+1) - 2 v_{lm}(n) + v_{lm}(n-1)}{T^2}} ... ...ft.\frac{v_{l+1,m}(n) - 2 v_{lm}(n) + v_{l-1,m}(n)}{X^2}\right]. \end{eqnarray*}
In the limit, as the sampling intervals $ X,Y,T$ approach zero such that $ X/T = Y/T$ remains constant, we recognize these expressions as the definitions of the partial derivatives with respect to $ t$, $ x$, and $ y$, respectively, yielding

$\displaystyle \frac{\partial^2 v(t,x,y)}{\partial t^2} = \frac{X^2}{2T^2} \left... ...^2 v(t,x,y)}{\partial x^2} + \frac{\partial^2 v(t,x,y)}{\partial y^2} \right]. $

This final result is the ideal 2D wave equation $ \ddot v = c^2 \nabla^2 v$, i.e.,

$\displaystyle \frac{\partial^2 v}{\partial t^2} = c^2 \left[ \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} \right] $

with

$\displaystyle c = \frac{1}{\sqrt{2}}\frac{X}{T} = \frac{\sqrt{2}}{2}\frac{X}{T}. \protect$ (C.118)

Discussion regarding solving the 2D wave equation subject to boundary conditions appears in §B.8.3. Interpreting this value for the wave propagation speed $ c$, we see that every two time steps of $ 2T$ seconds corresponds to a spatial step of $ \sqrt{2}X$ meters. This is the distance from one diagonal to the next in the square-hole mesh. We will show later that diagonal directions on the mesh support exact propagation (of plane waves traveling at 45-degree angles with respect to the $ x$ or $ y$ axes). In the $ x$ and $ y$ directions, propagation is highly dispersive, meaning that different frequencies travel at different speeds. The exactness of 45-degree angles can be appreciated by considering Huygens' principle on the mesh.
Next Section:
The Lossy 2D Mesh
Previous Section:
Recent Developments