DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Solving the 2D Wave Equation

Since solving the wave equation in 2D has all the essential features of the 3D case, we will look at the 2D case in this section.

Specializing Eq.$ \,$(B.47) to 2D, the 2D wave equation may be written as

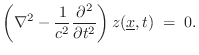
$\displaystyle \left(\nabla ^2 - \frac{1}{c^2}\frac{\partial^2}{\partial t^2} \right) z(\underline{x},t) \eqsp 0. $

where

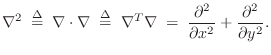
$\displaystyle \nabla ^2 \isdefs \nabla \cdot \nabla \isdefs \nabla ^T\nabla \eqsp \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2}. $

The 2D wave equation is obeyed by traveling sinusoidal plane waves having any amplitude $ A$, radian frequency $ \omega $, phase $ \phi$, and direction $ \underline{u}$:

$\displaystyle z(\underline{x},t) = A\,e^{j\phi}\,e^{j(\omega t - \underline{k}^T\underline{x})} $

where $ \underline{k}=k\underline{u}$ denotes the vector-wavenumber, $ k=\omega/c$ denotes the wavenumber (spatial radian frequency) of the wave along its direction of travel, and $ \underline{u}$ is a unit vector of direction cosines. This is the analytic-signal form of a sinusoidal traveling plane wave, and we may define the real (physical) signal as the real part of the analytic signal, as usual [451]. We see that the only constraint imposed by the wave equation on this general traveling-wave is the so-called dispersion relation:

$\displaystyle k\eqsp \vert\underline{k}\vert\eqsp \frac{\omega}{c} $

In particular, the wave can travel in any direction, with any amplitude, frequency, and phase. The only constraint is that its spatial frequency $ k$ is tied to its temporal frequency $ \omega $ by the dispersion relation.B.36

The sum of two such waves traveling in opposite directions with the same amplitude and frequency produces a standing wave. For example, if the waves are traveling parallel to the $ x$ axis, we have

$\displaystyle z(\underline{x},t) \eqsp A\,e^{j\phi}\,e^{j\omega t - kx} + A\,e^{j\phi}\,e^{j\omega t + kx} \eqsp 2A\,e^{j(\omega t + \phi)}\,\cos(kx) \protect$ (B.49)

which is a standing wave along $ x$.

Next Section:
2D Boundary Conditions
Previous Section:
Vector Wavenumber