Energy in the Mass-Spring Oscillator
Summarizing the previous sections, we say that a compressed spring holds a potential energy equal to the work required to compress the spring from rest to its current displacement. If a compressed spring is allowed to expand by pushing a mass, as in the system of Fig.B.2, the potential energy in the spring is converted to kinetic energy in the moving mass.
We can draw some inferences from the oscillatory motion of the
mass-spring system written in Eq.![]() (B.5):
(B.5):
- From a global point of view, we see that energy is conserved, since the oscillation never decays.
- At the peaks of the displacement
 (when
(when
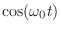 is either
is either
 or
or  ), all energy is in the form of potential energy,
i.e., the spring is either maximally compressed or stretched, and the mass
is momentarily stopped as it is changing direction.
), all energy is in the form of potential energy,
i.e., the spring is either maximally compressed or stretched, and the mass
is momentarily stopped as it is changing direction.
- At the zero-crossings of
 , the spring is momentarily
relaxed, thereby holding no potential energy; at these instants, all
energy is in the form of kinetic energy, stored in the motion of the mass.
, the spring is momentarily
relaxed, thereby holding no potential energy; at these instants, all
energy is in the form of kinetic energy, stored in the motion of the mass.
- Since total energy is conserved (§B.2.5), the kinetic
energy of the mass at the displacement zero-crossings is exactly the
amount needed to stretch the spring to displacement
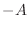 (or compress
it to
(or compress
it to 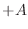 ) before the mass stops and changes direction. At all
times, the total energy
) before the mass stops and changes direction. At all
times, the total energy  is equal to the sum of the potential
energy
is equal to the sum of the potential
energy 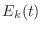 stored in the spring, and the kinetic energy
stored in the spring, and the kinetic energy 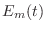 stored in the mass:
stored in the mass:
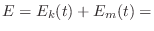
![$\displaystyle \mbox{constant [$E_k(0)$]}$](http://www.dsprelated.com/josimages_new/pasp/img2672.png)
Next Section:
Energy Conservation
Previous Section:
Mass Kinetic Energy from Virtual Work



















