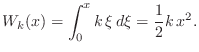Work = Force times Distance = Energy
Work is defined as force times distance. Work is a measure of the energy expended in applying a force to move an object.B.8
The work required to compress a spring ![]() through a displacement of
through a displacement of ![]() meters, starting from rest, is then
meters, starting from rest, is then
Work can also be negative. For example, when uncompressing an ideal spring, the (positive) work done by the spring on its moving end support can be interpreted also as saying that the end support performs negative work on the spring as it allows the spring to uncompress. When negative work is performed, the driving system is always accepting energy from the driven system. This is all simply accounting. Physically, one normally considers the driver as the agent performing the positive work, i.e., the one expending energy to move the driven object. Thus, when allowing a spring to uncompress, we consider the spring as performing (positive) work on whatever is attached to its moving end.
During a sinusoidal mass-spring oscillation, as derived in §B.1.4, each period of the oscillation can be divided into equal sections during which either the mass performs work on the spring, or vice versa.
Gravity, spring forces, and electrostatic forces are examples of
conservative forces. Conservative forces have the property
that the work required to move an object from point ![]() to point
to point ![]() ,
either with or against the force, depends only on the locations of
points
,
either with or against the force, depends only on the locations of
points ![]() and
and ![]() in space, not on the path taken from
in space, not on the path taken from ![]() to
to ![]() .
.
Potential Energy in a Spring
When compressing an ideal spring, work is performed, and this
work is stored in the spring in the form of what we call
potential energy. Equation (B.6) above gives the quantitative
formula for the potential energy ![]() stored in an ideal spring
after it has been compressed
stored in an ideal spring
after it has been compressed ![]() meters from rest.
meters from rest.
Kinetic Energy of a Mass
Kinetic energy is energy associated with motion. For example, when a spring uncompresses and accelerates a mass, as in the configuration of Fig.B.2, work is performed on the mass by the spring, and we say that the potential energy of the spring is converted to kinetic energy of the mass.
Suppose in Fig.B.2 we have an initial spring compression
by ![]() meters at time
meters at time ![]() , and the mass velocity is zero at
, and the mass velocity is zero at
![]() . Then from the equation of motion Eq.
. Then from the equation of motion Eq.![]() (B.5), we can calculate
when the spring returns to rest (
(B.5), we can calculate
when the spring returns to rest (![]() ). This first happens at the
first zero of
). This first happens at the
first zero of
![]() , which is time
, which is time
![]() . At this time, the velocity,
given by the time-derivative of Eq.
. At this time, the velocity,
given by the time-derivative of Eq.![]() (B.5),
(B.5),
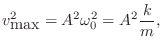
Mass Kinetic Energy from Virtual Work
From Newton's second law,
![]() (introduced in Eq.
(introduced in Eq.![]() (B.1)),
we can use d'Alembert's idea of virtual work to derive the
formula for the kinetic energy of a mass given its speed
(B.1)),
we can use d'Alembert's idea of virtual work to derive the
formula for the kinetic energy of a mass given its speed
![]() .
Let
.
Let ![]() denote a small (infinitesimal) displacement of the mass in
the
denote a small (infinitesimal) displacement of the mass in
the ![]() direction. Then we have, using the calculus of differentials,
direction. Then we have, using the calculus of differentials,
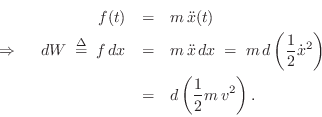
Thus, by Newton's second law, a differential of work ![]() applied to a
mass
applied to a
mass ![]() by force
by force ![]() through distance
through distance ![]() boosts the kinetic energy
of the mass by
boosts the kinetic energy
of the mass by
![]() . The kinetic energy of a mass moving at
speed
. The kinetic energy of a mass moving at
speed ![]() is then given by the integral of all such differential
boosts from 0 to
is then given by the integral of all such differential
boosts from 0 to ![]() :
:
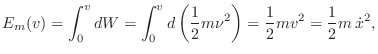
The quantity ![]() is classically called the virtual work
associated with force
is classically called the virtual work
associated with force ![]() , and
, and ![]() a virtual displacement
[544].
a virtual displacement
[544].
Energy in the Mass-Spring Oscillator
Summarizing the previous sections, we say that a compressed spring holds a potential energy equal to the work required to compress the spring from rest to its current displacement. If a compressed spring is allowed to expand by pushing a mass, as in the system of Fig.B.2, the potential energy in the spring is converted to kinetic energy in the moving mass.
We can draw some inferences from the oscillatory motion of the
mass-spring system written in Eq.![]() (B.5):
(B.5):
- From a global point of view, we see that energy is conserved, since the oscillation never decays.
- At the peaks of the displacement
 (when
(when
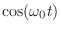 is either
is either
 or
or  ), all energy is in the form of potential energy,
i.e., the spring is either maximally compressed or stretched, and the mass
is momentarily stopped as it is changing direction.
), all energy is in the form of potential energy,
i.e., the spring is either maximally compressed or stretched, and the mass
is momentarily stopped as it is changing direction.
- At the zero-crossings of
 , the spring is momentarily
relaxed, thereby holding no potential energy; at these instants, all
energy is in the form of kinetic energy, stored in the motion of the mass.
, the spring is momentarily
relaxed, thereby holding no potential energy; at these instants, all
energy is in the form of kinetic energy, stored in the motion of the mass.
- Since total energy is conserved (§B.2.5), the kinetic
energy of the mass at the displacement zero-crossings is exactly the
amount needed to stretch the spring to displacement
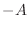 (or compress
it to
(or compress
it to 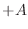 ) before the mass stops and changes direction. At all
times, the total energy
) before the mass stops and changes direction. At all
times, the total energy  is equal to the sum of the potential
energy
is equal to the sum of the potential
energy 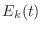 stored in the spring, and the kinetic energy
stored in the spring, and the kinetic energy 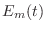 stored in the mass:
stored in the mass:
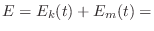
![$\displaystyle \mbox{constant [$E_k(0)$]}$](http://www.dsprelated.com/josimages_new/pasp/img2672.png)
Energy Conservation
It is a remarkable property of our universe that energy is conserved under all circumstances. There are no known exceptions to the conservation of energy, even when relativistic and quantum effects are considered.B.9
Energy may be defined as the ability to do work, where work may be defined as force times distance (§B.2).
Energy Conservation in the Mass-Spring System
Recall that Newton's second law applied to a mass-spring system, as in §B.1.4, yields
![\begin{eqnarray*}
0
&=& m{\ddot x}(t){\dot x}(t) + k\,x(t){\dot x}(t)\\
&=& m\...
...{d}{dt} \left[ E_m(t) + E_k(t) \right]\\
&=& \frac{d}{dt} E(t).
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img2682.png)
Thus, Newton's second law and Hooke's law imply conservation of energy in the mass-spring system of Fig.B.2.
Next Section:
Momentum
Previous Section:
Newton's Laws of Motion