Vector Cross Product
The vector cross product (or simply vector product, as
opposed to the scalar product (which is also called the
dot product, or inner product)) is commonly used in
vector calculus--a basic mathematical toolset used in
mechanics [270,258],
acoustics [349], electromagnetism [356], quantum
mechanics, and more. It can be defined symbolically in the form of
a matrix determinant:B.19
where
The second and third lines of Eq.![]() (B.15) make it clear that
(B.15) make it clear that
![]() . This is one example of a host of identities that
one learns in vector calculus and its applications.
. This is one example of a host of identities that
one learns in vector calculus and its applications.
Cross-Product Magnitude
It is a straightforward exercise to show that the cross-product magnitude is equal to the product of the vector lengths times the sine of the angle between them:B.21
where
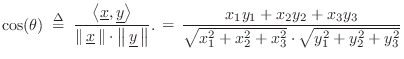
To derive Eq.![]() (B.16), let's begin with the cross-product in matrix
form as
(B.16), let's begin with the cross-product in matrix
form as
![]() using the first matrix form in the
third line of the cross-product definition in Eq.
using the first matrix form in the
third line of the cross-product definition in Eq.![]() (B.15) above. Then
(B.15) above. Then
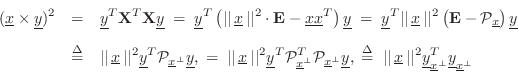
where
![]() denotes the identity matrix in
denotes the identity matrix in
![]() ,
,
![]() denotes the orthogonal-projection matrix onto
denotes the orthogonal-projection matrix onto
![]() [451],
[451],
![]() denotes the projection matrix onto
the orthogonal complement of
denotes the projection matrix onto
the orthogonal complement of
![]() ,
,
![]() denotes the component of
denotes the component of
![]() orthogonal to
orthogonal to
![]() , and we used the fact that orthogonal projection matrices
, and we used the fact that orthogonal projection matrices
![]() are idempotent (i.e.,
are idempotent (i.e.,
![]() ) and
symmetric (when real, as we have here) when we replaced
) and
symmetric (when real, as we have here) when we replaced
![]() by
by
![]() above. Finally,
note that the length of
above. Finally,
note that the length of
![]() is
is
![]() , where
, where ![]() is the angle
between the 1D subspaces spanned by
is the angle
between the 1D subspaces spanned by
![]() and
and
![]() in the plane
including both vectors. Thus,
in the plane
including both vectors. Thus,
The direction of the cross-product vector is then taken to be
orthogonal to both
![]() and
and
![]() according to the right-hand
rule. This orthogonality can be checked by verifying that
according to the right-hand
rule. This orthogonality can be checked by verifying that
![]() . The right-hand-rule parity can be checked by
rotating the space so that
. The right-hand-rule parity can be checked by
rotating the space so that
![]() and
and
![]() in
which case
in
which case
![]() . Thus, the cross
product points ``up'' relative to the
. Thus, the cross
product points ``up'' relative to the
![]() plane for
plane for
![]() and ``down'' for
and ``down'' for
![]() .
.
Mass Moment of Inertia as a Cross Product
In Eq.![]() (B.14) above, the mass moment of inertia was expressed
in terms of orthogonal projection as
(B.14) above, the mass moment of inertia was expressed
in terms of orthogonal projection as
![]() , where
, where
![]() . In terms of the vector cross
product, we can now express it as
. In terms of the vector cross
product, we can now express it as
Tangential Velocity as a Cross Product
Referring again to Fig.B.4, we can write the
tangential velocity vector
![]() as a vector cross product of
the angular-velocity vector
as a vector cross product of
the angular-velocity vector
![]() (§B.4.11) and the position
vector
(§B.4.11) and the position
vector
![]() :
:
To see this, let's first check its direction and then its magnitude. By the right-hand rule,
Next Section:
Angular Momentum
Previous Section:
Angular Velocity Vector








![$\displaystyle \left\vert \begin{array}{ccc}
\underline{e}_1 & \underline{e}_2 &...
...ine{e}_3\\ [2pt]
x_1 & x_2 & x_3\\ [2pt]
y_1 & y_2 & y_3
\end{array}\right\vert$](http://www.dsprelated.com/josimages_new/pasp/img2809.png)
![$\displaystyle \left[\begin{array}{ccc}
0 & -x_3 & x_2\\ [2pt]
x_3 & 0 & -x_1\\ ...
...}\right]
\left[\begin{array}{c} x_1 \\ [2pt] x_2 \\ [2pt] x_3\end{array}\right]$](http://www.dsprelated.com/josimages_new/pasp/img2811.png)











