DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

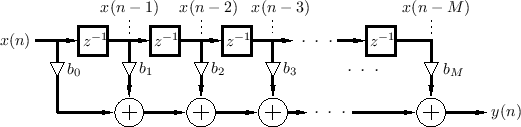
General Causal FIR Filters

The most general case--a TDL having a tap after every delay element--is the general causal Finite Impulse Response (FIR) filter, shown in Fig.2.22. It is restricted to be causal because the output $ y(n)$ may not depend on ``future'' inputs $ x(n+1)$, $ x(n+2)$, etc. The FIR filter is also called a transversal filter. FIR filters are described in greater detail in [449].

Figure 2.22: The general, causal, finite-impulse-response (FIR) digital filter.
\includegraphics{eps/fir}

The difference equation for the $ M$th-order FIR filter in Fig.2.22 is, by inspection,

$\displaystyle y(n) = b_0 x(n) + b_1 x(n-1) + b_2 x(n-2) + b_3 x(n-3) + \cdots + b_M x(n-M) $

and the transfer function is

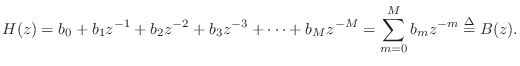
$\displaystyle H(z) = b_0 + b_1 z^{-1} + b_2 z^{-2} + b_3 z^{-3} + \cdots + b_M z^{-M} = \sum_{m=0}^M b_m z^{-m} \isdef B(z). $

The STK class for implementing arbitrary direct-form FIR filters is called Fir. (There is also a class for IIR filters named Iir.) In Matlab and Octave, the built-in function filter is normally used.

Next Section:
Feedforward Comb Filters
Previous Section:
TDL for Parallel Processing