DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

General Conditions for Losslessness

The scattering matrices for lossless physical waveguide junctions give an apparently unexplored class of lossless FDN prototypes. However, this is just a subset of all possible lossless feedback matrices. We are therefore interested in the most general conditions for losslessness of an FDN feedback matrix. The results below are adapted from [463,385].

Consider the general case in which $ \mathbf{A}$ is allowed to be any scattering matrix, i.e., it is associated with a not-necessarily-physical junction of $ N$ physical waveguides. Following the definition of losslessness in classical network theory, we may say that a waveguide scattering matrix $ \mathbf{A}$ is said to be lossless if the total complex power [35] at the junction is scattering invariant, i.e.,

$\displaystyle {\mathbf{p}^+}^\ast {\bm \Gamma}\mathbf{p}^+$ $\displaystyle =$ $\displaystyle {\mathbf{p}^-}^\ast {\bm \Gamma}\mathbf{p}^-$  
$\displaystyle \implies \quad \mathbf{A}^\ast {\bm \Gamma}\mathbf{A}$ $\displaystyle =$ $\displaystyle {\bm \Gamma} \protect$ (C.124)

where $ {\bm \Gamma}$ is any Hermitian, positive-definite matrix (which has an interpretation as a generalized junction admittance). The form $ x^\ast {\bm \Gamma} x$ is by definition the square of the elliptic norm of $ x$ induced by $ {\bm \Gamma}$, or $ \vert\vert\,x\,\vert\vert _{\bm \Gamma}^2 = x^\ast {\bm \Gamma}x$. Setting $ {\bm \Gamma}=\mathbf{I}$, we obtain that $ \mathbf{A}$ must be unitary. This is the case commonly used in current FDN practice.

The following theorem gives a general characterization of lossless scattering:

Theorem: A scattering matrix (FDN feedback matrix) $ \mathbf{A}$ is lossless if and only if its eigenvalues lie on the unit circle and its eigenvectors are linearly independent.

Proof: Since $ {\bm \Gamma}$ is positive definite, it can be factored (by the Cholesky factorization) into the form $ {\bm \Gamma}= \mathbf{U}^\ast \mathbf{U}$, where $ \mathbf{U}$ is an upper triangular matrix, and $ \mathbf{U}^\ast $ denotes the Hermitian transpose of $ \mathbf{U}$, i.e., $ \mathbf{U}^\ast \isdef \overline{\mathbf{U}}^T$. Since $ {\bm \Gamma}$ is positive definite, $ \mathbf{U}$ is nonsingular and can be used as a similarity transformation matrix. Applying the Cholesky decomposition $ {\bm \Gamma}= \mathbf{U}^\ast \mathbf{U}$ in Eq.$ \,$(C.125) yields

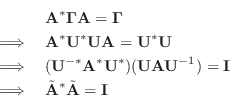
\begin{eqnarray*} & & \mathbf{A}^\ast {\bm \Gamma}\mathbf{A}= {\bm \Gamma}\\ &\... ...\implies& \tilde{\mathbf{A}}^\ast \tilde{\mathbf{A}}= \mathbf{I} \end{eqnarray*}

where $ \mathbf{U}^{-\ast}\isdef (\mathbf{U}^{-1})^\ast$, and

$\displaystyle \tilde{\mathbf{A}}\isdef \mathbf{U}\mathbf{A}\mathbf{U}^{-1} $

is similar to $ \mathbf{A}$ using $ \mathbf{U}^{-1}$ as the similarity transform matrix. Since $ \tilde{\mathbf{A}}$ is unitary, its eigenvalues have modulus 1. Hence, the eigenvalues of every lossless scattering matrix lie on the unit circle in the $ z$ plane. It readily follows from similarity to $ \tilde{\mathbf{A}}$ that $ \mathbf{A}$ admits $ N$ linearly independent eigenvectors. In fact, $ \tilde{\mathbf{A}}$ is a normal matrix ( $ \mathbf{A}\tilde{\mathbf{A}}= \tilde{\mathbf{A}}\mathbf{A}$), since every unitary matrix is normal, and normal matrices admit a basis of linearly independent eigenvectors [346].

Conversely, assume $ \vert\lambda\vert = 1$ for each eigenvalue of $ \mathbf{A}$, and that there exists a matrix $ \mathbf{E}$ of linearly independent eigenvectors of $ \mathbf{A}$. The matrix $ \mathbf{E}$ diagonalizes $ \mathbf{A}$ to give $ \mathbf{E}^{-1}\mathbf{A}\mathbf{E}= \mathbf{D}$, where $ \mathbf{D}=$   diag$ (\lambda_1,\dots,\lambda_N)$. Taking the Hermitian transform of this equation gives $ \mathbf{E}^\ast \mathbf{A}^\ast \mathbf{E}^{-\ast}= \mathbf{D}^\ast $. Multiplying, we obtain $ \mathbf{E}^\ast \mathbf{A}^\ast \mathbf{E}^{-\ast}\mathbf{E}^{-1}\mathbf{A}\ma... ...t \mathbf{E}^{-\ast}\mathbf{E}^{-1}\mathbf{A}=\mathbf{E}^{-\ast}\mathbf{E}^{-1}$. Thus, (C.125) is satisfied for $ {\bm \Gamma}=\mathbf{E}^{-\ast}\mathbf{E}^{-1}$ which is Hermitian and positive definite. $ \Box$

Thus, lossless scattering matrices may be fully parametrized as $ \mathbf{A} = \mathbf{E}^{-1}\mathbf{D}\mathbf{E}$, where $ \mathbf{D}$ is any unit-modulus diagonal matrix, and $ \mathbf{E}$ is any invertible matrix. In the real case, we have $ \mathbf{D}=$   diag$ (\pm 1)$ and $ \mathbf{E}\in\Re^{N\times N}$.

Note that not all lossless scattering matrices have a simple physical interpretation as a scattering matrix for an intersection of $ N$ lossless reflectively terminated waveguides. In addition to these cases (generated by all non-negative branch impedances), there are additional cases corresponding to sign flips and branch permutations at the junction. In terms of classical network theory [35], such additional cases can be seen as arising from the use of ``gyrators'' and/or ``circulators'' at the scattering junction [433]).

Next Section:
Gyrators
Previous Section:
Normalized Scattering