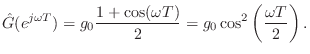Free Books    Physical Audio Signal Processing  

Length $ 3$ FIR Loop Filter Controlled by ``Brightness'' and ``Sustain''

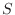Another convenient parametrization of the second-order symmetric FIR case is when the dc normalization is relaxed so that two degrees of freedom are retained. It is then convenient to control them as brightness $ B$ and sustain $ S$ according to the formulas

$\displaystyle g_0$ $\displaystyle =$ $\displaystyle \exp( - 6.91 P / S)$ (10.1)
$\displaystyle {\hat g}(0)$ $\displaystyle =$ $\displaystyle g_0 (1 + B)/2$ (10.2)
$\displaystyle {\hat g}(1)$ $\displaystyle =$ $\displaystyle g_0 (1 - B)/4 \protect$ (10.3)

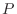
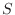
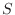
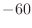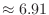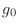
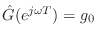
where $ P$ is the period in seconds (total loop delay), $ S$ is the desired sustain time in seconds, and $ B$ is the brightness parameter in the interval $ [0,1]$. The sustain parameter $ S$ is defined here as the time to decay by $ -60$ dB (or $ \approx 6.91$ time-constants) when brightness $ B$ is maximum ($ B=1$) in which case the loop gain is $ g_0$ at all frequencies, or $ {\hat G}(e^{j\omega T}) = g_0$. 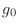As the brightness is lowered, the dc gain remains fixed at $ g_0$ while higher frequencies decay faster. At the minimum brightness, the gain at half the sampling rate reaches zero, and the loop-filter amplitude-response assumes the form

$\displaystyle {\hat G}(e^{j\omega T}) = g_0\frac{1 + \cos(\omega T)}{2} = g_0 \cos^2\left(\frac{\omega T}{2}\right). $

A Faust function implementing this FIR filter as the damping filter in the Extended Karplus Strong (EKS) algorithm is described in [454].

Next Section:
One-Zero Loop Filter
Previous Section:
Length Three FIR Loop Filter