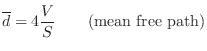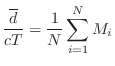Mean Free Path

A rough guide to the average delay-line length is the ``mean free path'' in the desired reverberant environment. The mean free path is defined as the average distance a ray of sound travels before it encounters an obstacle and reflects. An approximate value for the mean free path, due to Sabine, an early pioneer of statistical room acoustics, is

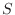
where is the total volume of the room, and is total surface area enclosing the room. This approximation requires the diffuse field assumption, i.e., that plane waves are traveling randomly in all directions [349,47] (see §3.2.1 for a simple construction). Normally, late reverberation satisfies this assumption well, away from open doors and windows, provided the room is not too ``dead''. Regarding each delay line as a mean-free-path delay, the average can be set to the mean free path by equating

where denotes sound speed and denotes the sampling period. This number should be treated as a lower bound because in real rooms reflections are often diffuse, especially at high frequencies. In a diffuse reflection, a single incident plane wave reflects in many directions at once.

---

Next Section:
Mode Density Requirement
Previous Section:
Triangular Feedback Matrices

Sign in