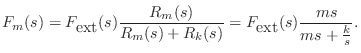Mechanical Impedance Analysis
Impedance analysis is commonly used to analyze electrical circuits [110]. By means of equivalent circuits, we can use the same analysis methods for mechanical systems.
For example, referring to Fig.7.9, the Laplace transform of
the force on the spring ![]() is given by the so-called voltage
divider relation:8.2
is given by the so-called voltage
divider relation:8.2
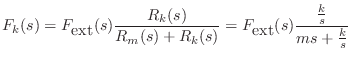
As a simple application, let's find the motion of the mass ![]() , after
time zero, given that the input force is an impulse at time 0:
, after
time zero, given that the input force is an impulse at time 0:
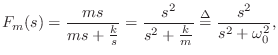
![\begin{eqnarray*}
V_m(s) &=& \frac{F_m(s)}{ms} \;=\; \frac{1}{m} \cdot \frac{s}{...
...}\right]\\ [5pt]
&\leftrightarrow& \frac{1}{m} \cos(\omega_0 t).
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/pasp/img1626.png)
Thus, the impulse response of the mass oscillates sinusoidally with
radian frequency
![]() , and amplitude
, and amplitude ![]() . The
velocity starts out maximum at time
. The
velocity starts out maximum at time ![]() , which makes physical sense.
Also, the momentum transferred to the mass at time 0 is
, which makes physical sense.
Also, the momentum transferred to the mass at time 0 is
![]() ;
this is also expected physically because the time-integral of the applied
force is 1 (the area under any impulse
;
this is also expected physically because the time-integral of the applied
force is 1 (the area under any impulse ![]() is 1).
is 1).
Next Section:
General One-Ports
Previous Section:
Spring-Mass System