Minimum Phase (MP) polynomials in 
All properties of MP polynomials apply without modification to marginally stable allpole transfer functions (cf. Property 2):
- Every first-order MP polynomial is positive real.
- Every first-order MP polynomial
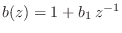 is such that
is such that
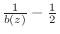 is positive real.
is positive real.
- A PR second-order MP polynomial with complex-conjugate zeros,
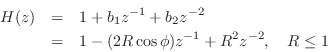
satisfies
If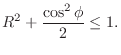
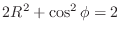 , then
re
, then
re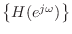 has a double zero at
has a double zero at
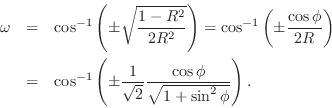
- All polynomials of the form
are positive real. (These have zeros uniformly distributed on a circle of radius
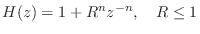
 .)
.)
Next Section:
Miscellaneous Properties
Previous Section:
Special cases and examples




















