Odd-Order Lagrange Interpolation Summary

In contrast to even-order Lagrange interpolation, the odd-order case has the following properties (in fractional delay filtering applications):

• Improved phase-delay accuracy at the expense of decreased amplitude-response accuracy (low-order examples in Fig.)
• Optimal (centered) delay range lies between two integers

The usual centered delay range is

---

---

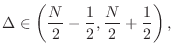
which is between integers, and in this range, the amplitude response is observed to be bounded by 1. To avoid a discontinuous phase-delay jump at high frequencies when crossing the middle delay, the delay range can be shifted to

but then the gain may exceed 1 at some frequencies.

---

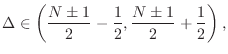
Next Section:
Proof of Maximum Flatness at DC
Previous Section:
Even-Order Lagrange Interpolation Summary

Sign in