Free Books
   Free Books    Physical Audio Signal Processing  


Proof of Maximum Flatness at DC

The maximumally flat fractional-delay FIR filter is obtained by equating to zero all $ N+1$ leading terms in the Taylor (Maclaurin) expansion of the frequency-response error at dc:

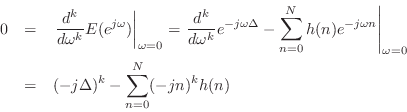
\begin{eqnarray*} 0 &=& \left.\frac{d^k}{d\omega^k} E(e^{j\omega}) \right\vert _... ...ert _{\omega=0}\\ &=& (-j\Delta)^k - \sum_{n=0}^N (-jn)^k h(n) \end{eqnarray*}

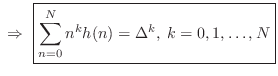
$\displaystyle \,\,\Rightarrow\,\,\zbox {\sum_{n=0}^N n^k h(n) = \Delta^k, \; k=0,1,\ldots,N} $

This is a linear system of equations of the form $ V\underline{h}=\underline{\Delta}$, where $ V$ is a Vandermonde matrix. The solution can be written as a ratio of Vandermonde determinants using Cramer's rule [329]. As shown by Cauchy (1812), the determinant of a Vandermonde matrix $ [p_i^{j-1}]$, $ i,j=1,\ldots,N$ can be expressed in closed form as

\begin{eqnarray*} \left\vert\left[p_i^{j-1}\right]\right\vert &=& \prod_{j>i}(p_... ...ts\\ &&(p_{N-1}-p_{N-2})(p_N-p_{N-2})\cdots\\ &&(p_N-p_{N-1}). \end{eqnarray*}

Making this substitution in the solution obtained by Cramer's rule yields that the impulse response of the order $ N$, maximally flat, fractional-delay FIR filter may be written in closed form as

$\displaystyle h(n) = \prod_{\stackrel{k=0}{k\ne n}}^N \frac{D-k}{n-k}, \quad n=0,1,\ldots N, $

which is the formula for Lagrange-interpolation coefficients (Eq.$ \,$(4.6)) adapted to this problem (in which abscissae are equally spaced on the integers from 0 to $ N-1$).

Further details regarding the theory of Lagrange interpolation can be found (online) in [502, Ch. 3, Pt. 2, pp. 82-84].

Next Section:
Variable Filter Parametrizations
Previous Section:
Odd-Order Lagrange Interpolation Summary