Parallel Combination of One-Ports

Figure Fig.7.10 shows the parallel combination of two one-ports.

**Figure 7.10:** Two one-port networks combined in parallel. The admittance of the parallel combination is $\Gamma (s) = \Gamma _1(s) + \Gamma _2(s)$ .
$\includegraphics[scale=0.9]{eps/lparallel}$

Admittances add in parallel, so the combined admittance is $\Gamma (s) = \Gamma _1(s) + \Gamma _2(s)$ , and the impedance is

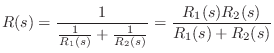
$\displaystyle R(s) = \frac{1}{\frac{1}{R_1(s)} + \frac{1}{R_2(s)}} = \frac{R_1(s) R_2(s) }{R_1(s) + R_2(s)}$

which is the familiar product-over-sum rule for combining impedances in parallel. This operation is often denoted by

$\displaystyle R= R_1 \vert\vert R_2$

Next Section:
Spring-Mass System
Previous Section:
Mass-Spring-Wall System

Sign in