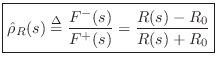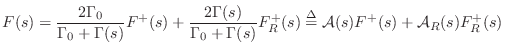DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Reflectance of a General Lumped Waveguide Termination

Calculate the reflectance of the terminated waveguide. That is, find the Laplace transform of the return wave divided by the Laplace transform of the input wave going into the waveguide. In general, the reflectance of an impedance step for force waves (voltage waves in the electrical case) is

$\displaystyle \fbox{$\displaystyle \hat{\rho}_R(s) \isdef \frac{F^{-}(s)}{F^{+}(s)} = \frac{R(s)-R_0}{R(s)+R_0}$} \protect$ (F.1)

This is easily derived from continuity constraints across the junction. Specifically, referring to Fig.F.1b, let $ F_R(s) = F^{+}_R(s) + F^{-}_R(s)$ denote the physical force and its traveling-wave components within the ``pseudo-infinitesimal-generalized-waveguide'' defined by the element impedance $ R(s)$, with the `$ +$' superscript denoting a right-going wave.F.1 Similarly, let $ V(s) = V^{+}(s)+V^{-}(s)$ denote the velocity and its component wave variables on the side of the junction at impedance $ R_0$, and let $ V_R(s) = V^{+}_R(s)+V^{-}_R(s)$ denote the corresponding quantities on the element-side of the junction at impedance $ R(s)$. Again, the `$ +$' superscript denotes travel to the right. Then the physical continuity constraints imply

\begin{eqnarray*} F(s) &=& F_R(s)\\ 0 &=& V(s) + V_R(s) \end{eqnarray*}

By the definition of wave impedance in a waveguide, we have

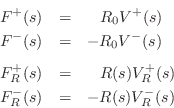
\begin{eqnarray*} F^{+}(s) &=& \quad\! R_0 V^{+}(s)\\ F^{-}(s) &=& - R_0 V^{-}(... ... &=& \quad\! R(s) V^{+}_R(s)\\ F^{-}_R(s) &=& - R(s) V^{-}_R(s) \end{eqnarray*}

Thus,

\begin{eqnarray*} 0 &=& V(s) + V_R(s)\\ &=& \left[V^{+}(s)+V^{-}(s)\right] + ... ...s)}\right] &=& \frac{2}{R_0}F^{+}(s) + \frac{2}{R(s)}F^{+}_R(s) \end{eqnarray*}

Defining $ \Gamma_0 \isdef 1/R_0$ and $ \Gamma(s) \isdef 1/R(s)$, we have

$\displaystyle F(s) = \frac{2\Gamma_0}{\Gamma_0+\Gamma(s)} F^{+}(s) + \frac{2\Ga... ...a(s)} F^{+}_R(s) \isdef {\cal A}(s) F^{+}(s) + {\cal A}_R(s)F^{+}_R(s) \protect$ (F.2)

Now that we've solved for the junction force $ F(s)$, the outgoing waves are simply obtained from the force continuity constraint, $ F(s) = F^{+}(s)+F^{-}(s) = F^{+}_R(s)+F^{-}_R(s)$:
$\displaystyle F^{-}(s)$ $\displaystyle =$ $\displaystyle F(s) - F^{+}(s) \protect$ (F.3)
$\displaystyle F^{-}_R(s)$ $\displaystyle =$ $\displaystyle F(s) - F^{+}_R(s) \protect$ (F.4)

Finally, the force-wave reflectance of an impedance step from $ R_0$ to $ R(s)$ can be found by solving Eq.$ \,$(F.3) and (F.2) for $ F^{-}(s)/F^{+}(s)$ with $ F^{+}_R(s)$ set to zero:

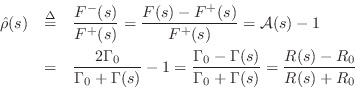
\begin{eqnarray*} \hat{\rho}(s) &\isdef & \frac{F^{-}(s)}{F^{+}(s)} = \frac{F(s)... ...mma_0-\Gamma(s)}{\Gamma_0+\Gamma(s)} = \frac{R(s)-R_0}{R(s)+R_0} \end{eqnarray*}

as claimed.

Next Section:
Reflectances of Elementary Impedances
Previous Section:
Interior Scattering Junctions