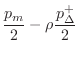Scattering-Theoretic Formulation
Equation (9.38) can be solved for ![]() to obtain
to obtain
where
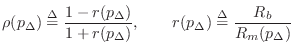 |
(10.44) |
We interpret
Since the mouthpiece of a clarinet is nearly closed,
![]() which
implies
which
implies
![]() and
and
![]() . In the limit as
. In the limit as ![]() goes to
infinity relative to
goes to
infinity relative to ![]() , (9.42) reduces to the simple form of a
rigidly capped acoustic tube, i.e.,
, (9.42) reduces to the simple form of a
rigidly capped acoustic tube, i.e.,
![]() .
If it were possible to open the reed wide enough to achieve
matched impedance,
.
If it were possible to open the reed wide enough to achieve
matched impedance, ![]() , then we would have
, then we would have ![]() and
and ![]() , in
which case
, in
which case
![]() , with no reflection of
, with no reflection of ![]() , as expected. If
the mouthpiece is removed altogether to give
, as expected. If
the mouthpiece is removed altogether to give ![]() (regarding it now as a
tube section of infinite radius), then
(regarding it now as a
tube section of infinite radius), then ![]() ,
, ![]() , and
, and
![]() .
.
Next Section:
Computational Methods
Previous Section:
Digital Waveguide Single-Reed Implementation