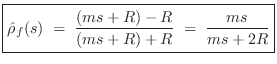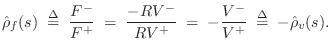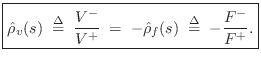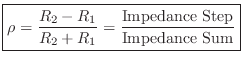Free Books
   Free Books    Physical Audio Signal Processing  

Simplified Impedance Analysis

The above results are quickly derived from the general reflection-coefficient for force waves (or voltage waves, pressure waves, etc.):

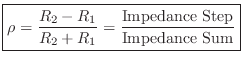$\displaystyle \zbox {\rho = \frac{R_2-R_1}{R_2+R_1} = \frac{\mbox{Impedance Step}}{\mbox{Impedance Sum}}} \protect$ (10.17)

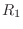
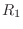
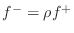
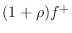
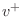
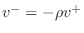
where $ \rho$ is the reflection coefficient of impedance $ R_2$ as ``seen'' from impedance $ R_1$. If a force wave $ f^{{+}}$ traveling along in impedance $ R_1$ suddenly hits a new impedance $ R_2$, the wave will split into a reflected wave $ f^{{-}}=\rho f^{{+}}$, and a transmitted wave $ (1+\rho)f^{{+}}$. 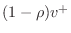It therefore follows that a velocity wave $ v^{+}$ will split into a reflected wave $ v^{-}= - \rho v^{+}$ and transmitted wave $ (1-\rho)v^{+}$. This rule is derived in §C.8.4 (and implicitly above as well).

In the mass-string-collision problem, we can immediately write down the force reflectance of the mass as seen from either string:

$\displaystyle \zbox {\hat{\rho}_f(s) \eqsp \frac{(ms+R) - R}{(ms+R) + R} \eqsp \frac{ms}{ms+2R}} $

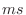
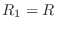
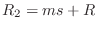
That is, waves in the string are traveling through wave impedance $ R$, and when they hit the mass, they are hitting the series combination of the mass impedance $ ms$ and the wave impedance $ R$ of the string on the other side of the mass. Thus, in terms of Eq.$ \,$(9.17) above, $ R_1=R$ and $ R_2=ms+R$.

Since, by the Ohm's-law relations,

$\displaystyle \hat{\rho}_f(s) \isdefs \frac{F^{-}}{F^{+}} \eqsp \frac{-RV^{-}}{RV^{+}} \eqsp - \frac{V^{-}}{V^{+}} \isdefs -\hat{\rho}_v(s). $

we have that the velocity reflectance is simply

$\displaystyle \zbox {\hat{\rho}_v(s) \isdefs \frac{V^{-}}{V^{+}} \eqsp -\hat{\rho}_f(s) \isdefs -\frac{F^{-}}{F^{+}}.} $

Next Section:
Mass Transmittance from String to String
Previous Section:
Mass Reflectance from Either String