Free Books
   Free Books    Physical Audio Signal Processing  

Mass Transmittance from String to String

Referring to Fig.9.15, the velocity transmittance from string 1 to string 2 may be defined as

$\displaystyle \hat{\tau}_v(s) \eqsp \frac{V^{+}_2(s)}{V^{+}_1(s)}. $

By physical symmetry, we expect the transmittance to be the same in the opposite direction: $ \hat{\tau}_v(s) = \frac{V^{-}_1(s)}{V^{-}_2(s)}$. Assuming the incoming wave $ V^{-}_2$ on string 2 is zero, we have $ V^{+}_2=V$, which we found in Eq.$ \,$(9.16):

$\displaystyle V \eqsp \frac{2R}{ms+2R}V^{+}_1 $

Thus, the mass transmittance for velocity waves is

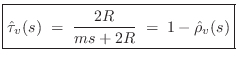
$\displaystyle \zbox {\hat{\tau}_v(s) \eqsp \frac{2R}{ms+2R} \eqsp 1-\hat{\rho}_v(s)} $

We see that $ m\to\infty$ corresponds to $ \hat{\tau}_v(s)\to 0$, as befits a rigid termination. As $ m\to0$, the transmittance becomes 1 and the mass has no effect, as desired.

We can now refine the picture of our scattering junction Fig.9.17 to obtain the form shown in Fig.9.18.

Figure 9.18: Velocity-wave scattering junction for a mass $ m$ (impedance $ ms$) attached to an ideal string having wave impedance $ R$.
\includegraphics[width=0.8\twidth]{eps/massstringdwmformvel}

Next Section:
Force Wave Mass-String Model
Previous Section:
Simplified Impedance Analysis