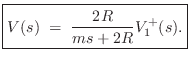Free Books
   Free Books    Physical Audio Signal Processing  

Mass Reflectance from Either String

Let's first consider how the mass looks from the viewpoint of string 1, assuming string 2 is at rest. In this situation (no incoming wave from string 2), string 2 will appear to string 1 as a simple resistor (or dashpot) of $ R$ Ohms in series with the mass impedance $ ms$. (This observation will be used as the basis of a rapid solution method in §9.3.1 below.)

When a wave from string 1 hits the mass, it will cause the mass to move. This motion carries both string endpoints along with it. Therefore, both the reflected and transmitted waves include this mass motion. We can say that we see a ``dispersive transmitted wave'' on string 2, and a dispersive reflection back onto string 1. Our object in this section is to calculate the transmission and reflection filters corresponding to these transmitted and reflected waves.

By physical symmetry the velocity reflection and transmission will be the same from string 1 as it is from string 2. We can say the same about force waves, but we will be more careful because the sign of the transverse force flips when the direction of travel is reversed.10.12Thus, we expect a scattering junction of the form shown in Fig.9.17 (recall the discussion of physically interacting waveguide inputs in §2.4.3). This much invokes the superposition principle (for simultaneous reflection and transmission), and imposes the expected symmetry: equal reflection filters $ \hat{\rho}(s)$ and equal transmission filters $ \hat{\tau}(s)$ (for either force or velocity waves).

Figure 9.17: Expected form of the scattering junction representing a mass $ m$ attached to the string. This form is expected for both force and velocity waves. The LTI filter transfer function $ \hat{\rho}(s)$ models the reflectance of the mass on the spring, while $ \hat{\tau}(s)$ models its transmittance.
\includegraphics[width=\twidth]{eps/massstringdwmform1}

Let's begin with Eq.$ \,$(9.12) above, restated as follows:

$\displaystyle 0 \eqsp f_m(t) + f_1(t,x_m) - f_2(t,x_m). \protect$ (10.14)

The traveling-wave decompositions can be written out as
$\displaystyle f_1(t,x_m)$ $\displaystyle =$ $\displaystyle f^{{+}}_1(t-x_m/c) + f^{{-}}_1(t+x_m/c)$  
$\displaystyle f_2(t,x_m)$ $\displaystyle =$ $\displaystyle f^{{+}}_2(t+x_m/c) + f^{{-}}_2(t-x_m/c) \protect$ (10.15)

where a ``+'' superscript means ``right-going'' and a ``-'' superscript means ``left-going'' on either string.10.13

Let's define the mass position $ x_m$ to be zero, so that Eq.$ \,$(9.14) with the substitutions Eq.$ \,$(9.15) becomes

$\displaystyle 0 \eqsp f_m(t) + [f^{{+}}_1(t) + f^{{-}}_1(t)] - [f^{{+}}_2(t)+f^{{-}}_2(t)] = 0. $

Let's now omit the common ``(t)'' arguments and write more simply

$\displaystyle f_m + f^{{+}}_1 + f^{{-}}_1 - f^{{+}}_2 - f^{{-}}_2 \eqsp 0. $

Let $ v=v_m=v_1=v_2$ denote the common velocity of the mass and string endpoints. Then we have $ f_m=-m\dot v$ for the mass (as discussed above at Eq.$ \,$(9.13)), and the Ohm's-law relations for the string are $ f^{{+}}_i=Rv^{+}_i$ and $ f^{{-}}_i=-Rv^{-}_i$. Making these substitutions gives

$\displaystyle -m\dot v+ Rv^{+}_1 -Rv^{-}_1 - Rv^{+}_2 + Rv^{-}_2 \eqsp 0. $

In the Laplace domain, dropping the common ``(s)'' arguments,

\begin{eqnarray*} F_m + F^{+}_1 + F^{-}_1 - F^{+}_2 -F^{-}_2 &=& 0\\ [10pt] \Lon... ...row\quad -msV + RV^{+}_1 - RV^{-}_1 - RV^{+}_2 + RV^{-}_2 &=& 0. \end{eqnarray*}

To compute the reflection coefficient of the mass seen on string 1, we may set $ V^{-}_2=0$, which means $ V=V^{+}_2+V^{-}_2=V^{+}_2$, so that we have

$\displaystyle -msV + RV^{+}_1 - RV^{-}_1 - RV\eqsp 0. $

Also, since $ V=V^{+}_1+V^{-}_1$, we can substitute $ V^{-}_1=V-V^{+}_1$ and solve for the common velocity to get

$\displaystyle \zbox {V(s) \eqsp \frac{2R}{ms+2R}V^{+}_1(s).} \protect$ (10.16)

From this, the reflected velocity is immediate:

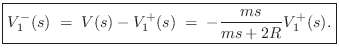
$\displaystyle \zbox {V^{-}_1(s) \eqsp V(s)-V^{+}_1(s) \eqsp -\frac{ms}{ms+2R}V^{+}_1(s).} $

The transmitted velocity is of course $ Vp_2(s)=V(s)$. We have thus found the velocity reflection transfer function (or velocity reflectance) of the mass as seen from string 1:

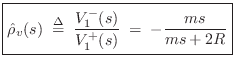
$\displaystyle \zbox {\hat{\rho}_v(s) \isdefs \frac{V^{-}_1(s)}{V^{+}_1(s)} \eqsp -\frac{ms}{ms+2R}} $

By physical symmetry, we also have $ V^{+}_2(s)/V^{-}_2(s) = \hat{\rho}_v(s)$, i.e., the transverse-velocity reflectance is the same on either side of the mass. Thus we have found both velocity reflection filters at the mass-string junction. In summary, the velocity reflectance of the mass is $ -ms/(ms+2R)$ from either string segment. This is a simple first-order filter model of what the mass (and string beyond) looks like dynamically from either string.

It is always good to check that our answers make physical sense in limiting cases. For this problem, easy cases to check are $ m=0$ and $ m=\infty$. When the mass is $ m=0$, the reflectance goes to zero (no reflected wave at all). When the mass goes to infinity, the reflectance approaches $ \hat{\rho}_v=-1$, corresponding to a rigid termination, which also makes sense.

The results of this section can be more quickly obtained as a special case of the main result of §C.12, by choosing $ N=2$ waveguides meeting at a load impedance $ R_J(s)=ms$. The next section gives another fast-calculation method based on a standard formula.

Next Section:
Simplified Impedance Analysis
Previous Section:
Mass Termination Model