DSPRelated.com
Free Books
   Free Books    Physical Audio Signal Processing  

Time-Varying Delay-Line Reads

If $ x(t)$ denotes the input to a time-varying delay, the output can be written as

$\displaystyle y(t)=x(t-D_t). $

where $ D_t$ denotes the time-varying delay in seconds. In discrete-time implementations, when $ D_t$ is not an integer multiple of the sampling interval, $ x(t-D_t)$ may be approximated to arbitrary accuracy (in a finite band) using bandlimited interpolation (see §4.4) or other techniques for implementation of fractional delay [267,383].

Let's analyze the frequency shift caused by a time-varying delay by setting $ x(t)$ to a complex sinusoid at frequency $ \omega_s $:

$\displaystyle x(t) = e^{j\omega_s t} $

The output is now

$\displaystyle y(t)= x(t-D_t) = e^{j\omega_s \cdot (t-D_t)}. $

The instantaneous phase of this signal is

$\displaystyle \theta(t)= \angle y(t) = \omega_s \cdot(t-D_t) $

which can be differentiated to give the instantaneous frequency

$\displaystyle \omega_l = \omega_s ( 1 - {\dot D_t}) \protect$ (6.6)

where $ \omega_l $ denotes the output frequency, and $ {\dot D_t}\isdef \frac{d}{dt}D_t$ denotes the time derivative of the delay $ D_t$. Thus, the delay growth-rate, $ {\dot D_t}$, equals the relative frequency downshift:

$\displaystyle {\dot D_t}= \frac{\omega_s -\omega_l }{\omega_s }. $

Comparing Eq.$ \,$(5.6) to Eq.$ \,$(5.2), we find that the time-varying delay most naturally simulates Doppler shift caused by a moving listener, with

$\displaystyle {\dot D_t}= -\frac{v_{ls}}{c}. \protect$ (6.7)

That is, the delay growth-rate, $ {\dot D_t}$, should be set to the speed of the listener away from the source, normalized by sound speed $ c$.

Simulating source motion is also possible, but the relation between delay change and desired frequency shift is more complex, viz., from Eq.$ \,$(5.2) and Eq.$ \,$(5.6),

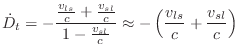
$\displaystyle {\dot D_t}= - \frac{\frac{v_{ls}}{c} + \frac{v_{sl}}{c}}{1-\frac{v_{sl}}{c}} \approx - \left(\frac{v_{ls}}{c} + \frac{v_{sl}}{c}\right) $

where the approximation is valid for $ v_{sl}\ll c$. In Section 5.7.4, a simplified approach is proposed based on moving the delay input instead of its output.

The time-varying delay line was described in §5.1. As discussed there, to implement a continuously varying delay, we add a ``delay growth parameter'' g to the delayline function in Fig.5.1, and change the line

  rptr += 1; // pointer update
to
  rptr += 1 - g; // pointer update
When g is 0, we have a fixed delay line, corresponding to $ {\dot D_t}=0$ in Eq.$ \,$(5.6). When $ \texttt{g}>0$, the delay grows $ \texttt{g}$ samples per sample, which we may also interpret as seconds per second, i.e., $ {\dot D_t}=\texttt{g}$. By Eq.$ \,$(5.7), we see that we need

$\displaystyle \texttt{g} = -\frac{v_{ls}}{c} $

to simulate a listener traveling toward the source at speed $ v_{ls}$.

Note that when the read- and write-pointers are driven directly from a model of physical propagation-path geometry, they are always separated by predictable minimum and maximum delay intervals. This implies it is unnecessary to worry about the read-pointer passing the write-pointers or vice versa. In generic frequency shifters [275], or in a Doppler simulator not driven by a changing geometry, a pointer cross-fade scheme may be necessary when the read- and write-pointers get too close to each other.

Next Section:
Multiple Read Pointers
Previous Section:
Doppler Simulation via Delay Lines