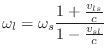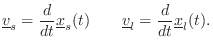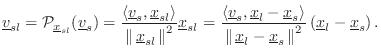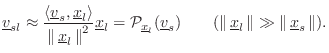Doppler Effect
The Doppler effect causes the pitch of a sound source to appear to rise or fall due to motion of the source and/or listener relative to each other. You have probably heard the pitch of a horn drop lower as it passes by (e.g., from a moving train). As a pitched sound-source moves toward you, the pitch you hear is raised; as it moves away from you, the pitch is lowered. The Doppler effect has been used to enhance the realism of simulated moving sound sources for compositional purposes [80], and it is an important component of the ``Leslie effect'' (described in §5.9).
As derived in elementary physics texts, the Doppler shift is given by
where
Vector Formulation
Denote the sound-source velocity by
![]() where
where
![]() is time. Similarly,
let
is time. Similarly,
let
![]() denote the velocity of the listener, if any. The
position of source and listener are denoted
denote the velocity of the listener, if any. The
position of source and listener are denoted
![]() and
and
![]() , respectively, where
, respectively, where
![]() is 3D
position. We have velocity related to position by
is 3D
position. We have velocity related to position by
Consider a Fourier component of the source at frequency
The Doppler effect depends only on velocity components along the line
connecting the source and listener [349, p. 453]. We may
therefore orthogonally project the source and listener
velocities onto the vector
![]() pointing from the source
to the listener. (See Fig.5.8 for a specific example.)
pointing from the source
to the listener. (See Fig.5.8 for a specific example.)
The orthogonal projection of a vector
![]() onto a vector
onto a vector
![]() is given by [451]
is given by [451]

In the far field (listener far away), Eq.
Next Section:
Doppler Simulation
Previous Section:
Vibrato Simulation