Tonal Correction Filter

Let denote the component of the impulse response arising from the th pole of the system. Then the energy associated with that pole is

All other factors being equal, if the decay time of the mode is shortened by half, it follows that the total energy contributed by that mode to the impulse response is also reduced by half. To compensate for this effect, Jot introduced a tonal correction filter to be placed in series with the FDN, as shown in Fig.3.10.

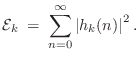
In the case of the first-order delay-line filters discussed in §3.7.5, good tonal correction is given by the following one-zero filter:

where

and is defined in Eq.(3.10).

---

Next Section:
FDNs as Digital Waveguide Networks
Previous Section:
Spectral Coloration Equalizer

Sign in