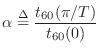Orthogonalized First-Order Delay-Filter Design

In [217], first-order delay-line filters of the form

$\displaystyle H_i(z) \eqsp g'_i \frac{1-p_i}{1-p_iz^{-1}}$

are proposed. Clearly $g_i=g'_i\cdot(1-p_i)$ . This form has the advantage that the dc gain is always

for all (stable) values of

. Therefore, we can set

to give a desired reverberation time at dc, and not have to change it when

is varied to modulate the high-frequency decay rate. As in the previous section, from Eq. $\,$ (3.9), we obtain

$\displaystyle g'_i \eqsp 10^{-3 M_i T / t_{60}(0)}.$

A calculation given in [217] arrives at

$\displaystyle p_i \eqsp \frac{\mbox{ln}(10)}{4}\log_{10}(g_i)\left(1-\frac{1}{\alpha^2}\right)$

where

$\displaystyle \alpha \isdef \frac{t_{60}(\pi/T)}{t_{60}(0)} \protect$

(4.10)

denotes the ratio of reverberation time at half the sampling rate divided by the reverberation time at dc.^4.16

Next Section:
Multiband Delay-Filter Design
Previous Section:
First-Order Delay-Filter Design

Sign in