DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Chirplet Fourier Transform

The Fourier transform of a complex Gaussian pulse is derived in §D.8 of Appendix D:

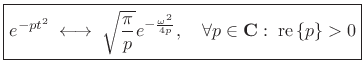$\displaystyle \zbox {e^{-pt^2} \;\longleftrightarrow\;\sqrt{\frac{\pi}{p}} e^{-\frac{\omega^2}{4p}},\quad \forall p\in {\bf C}: \; \mbox{re}\left\{p\right\}>0} \protect$ (11.27)

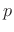
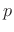
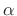
This result is valid when $ p$ is complex. Writing $ p$ in terms of real variables $ \alpha $ and $ \beta $ as

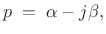$\displaystyle p \eqsp \alpha - j\beta,$ (11.28)

we have

$\displaystyle x(t) \eqsp e^{-p t^2} \eqsp e^{-\alpha t^2} e^{j\beta t^2} \eqsp e^{-\alpha t^2} \left[\cos(\beta t^2) + j\sin(\beta t^2)\right].$ (11.29)

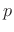
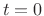
That is, for $ p$ complex, $ x(t)$ is a chirplet (Gaussian-windowed chirp). We see that the chirp oscillation frequency is zero at time $ t=0$ . Therefore, for signal modeling applications, we typically add in an arbitrary frequency offset at time 0, as described in the next section.

Next Section:
Modulated Gaussian-Windowed Chirp
Previous Section:
Further Reading