DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Gaussian Function Properties

This appendix collects together various facts about the fascinating Gaussian function--the classic ``bell curve'' that arises repeatedly in science and mathematics. As already seen in §B.17.1, only the Gaussian achieves the minimum time-bandwidth product among all smooth (analytic) functions.

Gaussian Window and Transform

The Gaussian window for FFT analysis was introduced in §3.11, and complex Gaussians (``chirplets'') were utilized in §10.6. For reference in support of these topics, this appendix derives some additional properties of the Gaussian, defined by

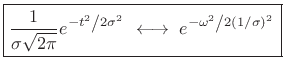$\displaystyle \zbox { \frac{1}{\sigma\sqrt{2\pi}}e^{-t^2 \left / 2\sigma^2\right.} \;\longleftrightarrow\; e^{-\omega^2 \left/ 2\left(1/\sigma\right)^2\right.} } % zbox $ (D.1)

and discusses some interesting applications in spectral modeling (the subject of §10.4). The basic mathematics rederived here are well known (see, e.g., [202,5]), while the application to spectral modeling of sound remains a topic under development.

Gaussians Closed under Multiplication

Define

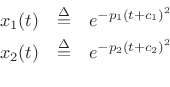
\begin{eqnarray*} x_1(t) &\isdef & e^{-p_1(t+c_1)^2}\\ x_2(t) &\isdef & e^{-p_2(t+c_2)^2}\\ \end{eqnarray*}

where $ p_1,p_2,c_1,c_2$ are arbitrary complex numbers. Then by direct calculation, we have

\begin{eqnarray*} x_1(t)\cdot x_2(t) &=& e^{-p_1(t+c_1)^2} e^{-p_2(t+c_2)^2}\\ &=& e^{-p_1 t^2 - 2 p_1 c_1 t - p_1 c_1^2 -p_2 t^2 - 2 p_2 c_2 t - p_2 c_2^2}\\ &=& e^{-(p_1+p_2) t^2 - 2 (p_1 c_1 + p_2 c_2) t - (p_1 c_1^2 + p_2 c_2^2)}\\ &=& e^{-(p_1+p_2)\left[t^2 + 2\frac{p_1 c_1 + p_2 c_2}{p_1 + p_2} t + \frac{p_1 c_1^2 + p_2 c_2^2}{p_1 + p_2}\right]} \end{eqnarray*}

Completing the square, we obtain

$\displaystyle x_1(t)\cdot x_2(t) = g \cdot e^{-p(t+c)^2}$ (D.2)

with

\begin{eqnarray*} p &=& p_1+p_2\\ [5pt] c &=& \frac{p_1 c_1 + p_2 c_2}{p_1 + p_2}\\ [5pt] g &=& e^{-p_1 p_2 \frac{(c_1 - c_2)^2}{p_1 + p_2}} \end{eqnarray*}

Note that this result holds for Gaussian-windowed chirps ($ p$ and $ c$ complex).

Product of Two Gaussian PDFs

For the special case of two Gaussian probability densities,

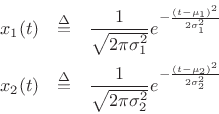
\begin{eqnarray*} x_1(t) &\isdef & \frac{1}{\sqrt{2\pi\sigma_1^2}}e^{-\frac{(t-\mu_1)^2}{2\sigma_1^2}}\\ x_2(t) &\isdef & \frac{1}{\sqrt{2\pi\sigma_2^2}}e^{-\frac{(t-\mu_2)^2}{2\sigma_2^2}} \end{eqnarray*}

the product density has mean and variance given by

\begin{eqnarray*} \mu &=& \frac{\frac{\mu_1}{2\sigma_1^2} + \frac{\mu_2}{2\sigma_2^2}}{\frac{1}{2\sigma_1^2} + \frac{1}{2\sigma_2^2}} \;\eqsp \; \frac{\mu_1\sigma_2^2 + \mu_2\sigma_1^2}{\sigma_2^2 + \sigma_1^2}\\ [5pt] \sigma^2 &=& \left. \sigma_1^2 \right\Vert \sigma_2^2 \;\isdefs \; \frac{1}{\frac{1}{\sigma_1^2} + \frac{1}{\sigma_2^2}} \;\eqsp \; \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2 + \sigma_2^2}. \end{eqnarray*}

Gaussians Closed under Convolution

In §D.8 we show that

  • the Fourier transform of a Gaussian is Gaussian, and in §D.2 that
  • the product of any two Gaussians is Gaussian.
Therefore, it follows from the convolution theorem for Fourier transforms (§B.7) that the convolution of any two Gaussians is Gaussian.

Fitting a Gaussian to Data

When fitting a single Gaussian to data, one can take a log and fit a parabola. In matlab, this can be carried out as in the following example:

x = -1:0.1:1;
sigma = 0.01;
y = exp(-x.*x) + sigma*randn(size(x)); % test data:
[p,s] = polyfit(x,log(y),2); % fit parabola to log
yh = exp(polyval(p,x)); % data model
norm(y-yh) % ans =  1.9230e-16 when sigma=0
plot(abs([y',yh']));
In practice, it is good to avoid zeros in the data. For example, one can fit only to the middle third or so of a measured peak, restricting consideration to measured samples that are positive and ``look Gaussian'' to a reasonable extent.

Infinite Flatness at Infinity

The Gaussian is infinitely flat at infinity. Equivalently, the Maclaurin expansion (Taylor expansion about $ t=0$ ) of

$\displaystyle f(t) = e^{-\frac{1}{t^2}}$ (D.3)

is zero for all orders. Thus, even though $ f(t)$ is differentiable of all orders at $ t=0$ , its series expansion fails to approach the function. This happens because $ e^{t^2}$ has an essential singularity at $ t=\infty$ (also called a ``non-removable singularity''). One can think of an essential singularity as an infinite number of poles piled up at the same point ($ t=\infty$ for $ e^{t^2}$ ). Equivalently, $ f(t)$ above has an infinite number of zeros at $ t=0$ , leading to the problem with Maclaurin series expansion. To prove this, one can show

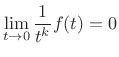$\displaystyle \lim_{t\to 0} \frac{1}{t^k} f(t) = 0$ (D.4)

for all $ k=1,2,\dots\,$ . This follows from the fact that exponential growth or decay is faster than polynomial growth or decay. An exponential can in fact be viewed as an infinite-order polynomial, since

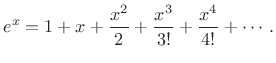$\displaystyle e^x=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots.$ (D.5)

We may call $ f(t) = e^{-\frac{1}{t^2}}$ infinitely flat at $ t=0$ in the ``Padé sense'':

Another interesting mathematical property of essential singularities is that near an essential singular point $ z_0\in{\bf C}$ the inequality

$\displaystyle \left\vert f(z)-c\right\vert<\epsilon$ (D.6)

is satisfied at some point $ z\neq z_0$ in every neighborhood of $ z_0$ , however small. In other words, $ f(z)$ comes arbitrarily close to every possible value in any neighborhood about an essential singular point. This was first proved by Weierstrass [42, p. 270].

Integral of a Complex Gaussian


Theorem:

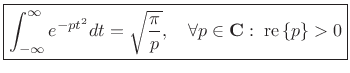$\displaystyle \zbox {\int_{-\infty}^\infty e^{-p t^2}dt = \sqrt{\frac{\pi}{p}}, \quad \forall p\in {\bf C}: \; \mbox{re}\left\{p\right\}>0}$ (D.7)


Proof: Let $ I(p)$ denote the integral. Then

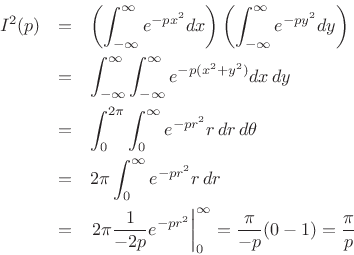
\begin{eqnarray*} I^2(p) &=& \left(\int_{-\infty}^\infty e^{-p x^2}dx\right) \left(\int_{-\infty}^\infty e^{-p y^2}dy\right)\\ &=& \int_{-\infty}^\infty \int_{-\infty}^\infty e^{-p (x^2+y^2)}dx\,dy\\ &=& \int_0^{2\pi}\int_0^\infty e^{-p r^2}r\,dr\,d\theta\\ &=& 2\pi\int_0^\infty e^{-p r^2}r\,dr\\ &=& \left. 2\pi\frac{1}{-2p} e^{-p r^2}\right\vert _0^\infty = \frac{\pi}{-p} (0 - 1) = \frac{\pi}{p} \end{eqnarray*}

where we needed re$ \left\{p\right\}>0$ to have $ e^{-p r^2}\to 0$ as $ r\to\infty$ . Thus,

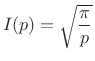$\displaystyle I(p) = \sqrt{\frac{\pi}{p}}$ (D.8)

as claimed.

Area Under a Real Gaussian


Corollary: Setting $ p=1/(2\sigma^2)$ in the previous theorem, where $ \sigma>0$ is real, we have

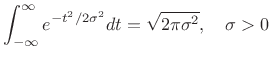$\displaystyle \int_{-\infty}^\infty e^{-t^2/2\sigma^2}dt = \sqrt{2\pi\sigma^2}, \quad \sigma>0$ (D.9)

Therefore, we may normalize the Gaussian to unit area by defining

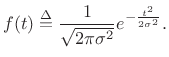$\displaystyle f(t) \isdef \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{t^2}{2\sigma^2}}.$ (D.10)

Since

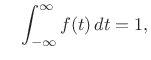$\displaystyle f(t)>0\;\forall t$   and$\displaystyle \quad \int_{-\infty}^\infty f(t)\,dt = 1,$ (D.11)

it satisfies the requirements of a probability density function.

Gaussian Integral with Complex Offset


Theorem:

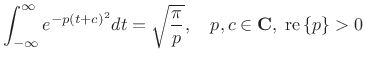$\displaystyle \int_{-\infty}^\infty e^{-p(t+c)^2}dt = \sqrt{\frac{\pi}{p}}, \quad p,c\in {\bf C},\;\mbox{re}\left\{p\right\}>0$ (D.12)


Proof: When $ c=0$ , we have the previously proved case. For arbitrary $ c=a+jb\in{\bf C}$ and real number $ T>\left\vert a\right\vert$ , let $ \Gamma_c(T)$ denote the closed rectangular contour $ z = (-T) \to T \to (T+jb) \to (-T+jb) \to (-T)$ , depicted in Fig.D.1.

Figure D.1: Contour of integration in the complex plane.
\includegraphics[width=0.8\twidth]{eps/gammarect}

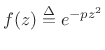Clearly, $ f(z) \isdef e^{-pz^2}$ is analytic inside the region bounded by $ \Gamma_c(T)$ . By Cauchy's theorem [42], the line integral of $ f(z)$ along $ \Gamma_c(T)$ is zero, i.e.,

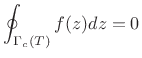$\displaystyle \oint_{\Gamma_c(T)} f(z) dz = 0$ (D.13)

This line integral breaks into the following four pieces:

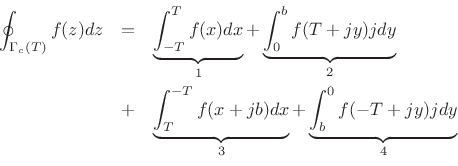
\begin{eqnarray*} \oint_{\Gamma_c(T)} f(z) dz &=& \underbrace{\int_{-T}^T f(x) dx}_1 + \underbrace{\int_{0}^{b} f(T+jy) jdy}_2\\ &+& \underbrace{\int_{T}^{-T} f(x+jb) dx}_3 + \underbrace{\int_{b}^{0} f(-T+jy) jdy}_4\\ \end{eqnarray*}

where $ x$ and $ y$ are real variables. In the limit as $ T\to\infty$ , the first piece approaches $ \sqrt{\pi/p}$ , as previously proved. Pieces $ 2$ and $ 4$ contribute zero in the limit, since $ e^{-p(t+c)^2} \to 0$ as $ \left\vert t\right\vert\to\infty$ . Since the total contour integral is zero by Cauchy's theorem, we conclude that piece 3 is the negative of piece 1, i.e., in the limit as $ T\to\infty$ ,

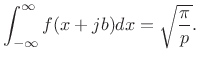$\displaystyle \int_{-\infty}^\infty f(x+jb) dx = \sqrt{\frac{\pi}{p}}.$ (D.14)

Making the change of variable $ x=t+a=t+c-jb$ , we obtain

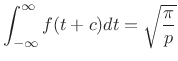$\displaystyle \int_{-\infty}^\infty f(t+c) dt = \sqrt{\frac{\pi}{p}}$ (D.15)

as desired.

Fourier Transform of Complex Gaussian


Theorem:

$\displaystyle \zbox {e^{-pt^2} \;\longleftrightarrow\;\sqrt{\frac{\pi}{p}} \, e^{-\frac{\omega^2}{4p}},\quad \forall p\in {\bf C}: \; \mbox{re}\left\{p\right\}>0}$ (D.16)


Proof: [202, p. 211] The Fourier transform of $ e^{-pt^2}$ is defined as

$\displaystyle \int_{-\infty}^\infty e^{-pt^2} e^{-j\omega t}dt \eqsp \int_{-\infty}^\infty e^{-(pt^2+j\omega t)} dt.$ (D.17)

Completing the square of the exponent gives

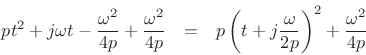
\begin{eqnarray*} pt^2 + j\omega t - \frac{\omega^2}{4p} + \frac{\omega^2}{4p} &=& p\left(t+j\frac{\omega}{2p}\right)^2 + \frac{\omega^2}{4p} \end{eqnarray*}

Thus, the Fourier transform can be written as

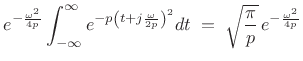$\displaystyle e^{-\frac{\omega^2}{4p}} \int_{-\infty}^\infty e^{-p\left(t+j\frac{\omega}{2p}\right)^2} dt \eqsp \sqrt{\frac{\pi}{p}}\, e^{-\frac{\omega^2}{4p}}$ (D.18)

using our previous result.

Alternate Proof

The Fourier transform of a complex Gaussian can also be derived using the differentiation theorem and its dual (§B.2).D.1


Proof: Let

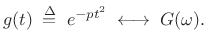$\displaystyle g(t)\isdefs e^{-pt^2} \;\longleftrightarrow\;G(\omega).$ (D.19)

Then by the differentiation theorem (§B.2),

$\displaystyle g^\prime(t) \;\longleftrightarrow\;j\omega G(\omega).$ (D.20)

By the differentiation theorem dual (§B.3),

$\displaystyle -jtg(t) \;\longleftrightarrow\;G^\prime(\omega).$ (D.21)

Differentiating $ g(t)$ gives

$\displaystyle g^\prime(t) \eqsp -2ptg(t) \eqsp \frac{2p}{j}[-jtg(t)] \;\longleftrightarrow\;\frac{2p}{j}G^\prime(\omega).$ (D.22)

Therefore,

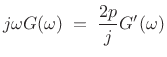$\displaystyle j\omega G(\omega) \eqsp \frac{2p}{j}G^\prime(\omega)$ (D.23)

or

$\displaystyle \left[\ln G(\omega)\right]^\prime \eqsp \frac{G^\prime(\omega)}{G(\omega)} \eqsp -\frac{\omega}{2p} \eqsp \left(-\frac{\omega^2}{4p}\right)^\prime.$ (D.24)

Integrating both sides with respect to $ \omega$ yields

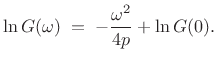$\displaystyle \ln G(\omega) \eqsp -\frac{\omega^2}{4p} + \ln G(0).$ (D.25)

In §D.7, we found that $ G(0)=\sqrt{\pi/p}$ , so that, finally, exponentiating gives

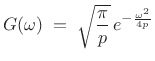$\displaystyle G(\omega) \eqsp \sqrt{\frac{\pi}{p}}\,e^{-\frac{\omega^2}{4p}}$ (D.26)

as expected.

The Fourier transform of complex Gaussians (``chirplets'') is used in §10.6 to analyze Gaussian-windowed ``chirps'' in the frequency domain.

Why Gaussian?

This section lists some of the points of origin for the Gaussian function in mathematics and physics.

Central Limit Theorem

The central limit theoremD.2provides that many iterated convolutions of any ``sufficiently regular'' shape will approach a Gaussian function.

Iterated Convolutions

Any ``reasonable'' probability density function (PDF) (§C.1.3) has a Fourier transform that looks like $ S(\omega) = 1 - \alpha \omega^2$ near its tip. Iterating $ N$ convolutions then corresponds to $ S^N(\omega)$ , which becomes [2]

$\displaystyle S^N(\omega) = (1-\alpha \omega^2)^N = \left(1-\frac{N\alpha \omega^2}{N}\right)^N \approx e^{-N\alpha\omega^2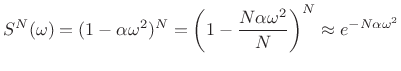}$ (D.27)

for large $ N$ , by the definition of $ e$ [264]. This proves that the $ N$ th power of $ 1-\alpha\omega^2$ approaches the Gaussian function defined in §D.1 for large $ N$ .

Since the inverse Fourier transform of a Gaussian is another Gaussian (§D.8), we can define a time-domain function $ s(t)$ as being ``sufficiently regular'' when its Fourier transform approaches $ S(\omega)\approx 1-\alpha\omega^2$ in a sufficiently small neighborhood of $ \omega = 0$ . That is, the Fourier transform simply needs a ``sufficiently smooth peak'' at $ \omega = 0$ that can be expanded into a convergent Taylor series. This obviously holds for the DTFT of any discrete-time window function $ w(n)$ (the subject of Chapter 3), because the window transform $ W(\omega)$ is a finite sum of continuous cosines of the form $ w(n)\cos(n\omega T)$ in the zero-phase case, and complex exponentials in the causal case, each of which is differentiable any number of times in $ \omega$ .

Binomial Distribution

The last row of Pascal's triangle (the binomial distribution) approaches a sampled Gaussian function as the number of rows increases.D.3 Since Lagrange interpolation (elementary polynomial interpolation) is equal to binomially windowed sinc interpolation [301,134], it follows that Lagrange interpolation approaches Gaussian-windowed sinc interpolation at high orders.

Gaussian Probability Density Function

Any non-negative function which integrates to 1 (unit total area) is suitable for use as a probability density function (PDF) (§C.1.3). The most general Gaussian PDF is given by shifts of the normalized Gaussian:

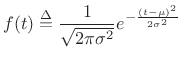$\displaystyle f(t) \isdef \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(t-\mu)^2}{2\sigma^2}}$ (D.28)

The parameter $ \mu$ is the mean, and $ \sigma^2$ is the variance of the distribution (we'll show this in §D.12 below).

Maximum Entropy Property of the
Gaussian Distribution

Entropy of a Probability Distribution

The entropy of a probability density function (PDF) $ p(x)$ is defined as [48]

$\displaystyle \zbox {h(p) \isdef \int_x p(x) \cdot \lg\left[\frac{1}{p(x)}\right] dx}$ (D.29)

where $ \lg$ denotes the logarithm base 2. The entropy of $ p(x)$ can be interpreted as the average number of bits needed to specify random variables $ x$ drawn at random according to $ p(x)$ :

$\displaystyle h(p) = {\cal E}_p\left\{\lg \left[\frac{1}{p(x)}\right]\right\}$ (D.30)

The term $ \lg[1/p(x)]$ can be viewed as the number of bits which should be assigned to the value $ x$ . (The most common values of $ x$ should be assigned the fewest bits, while rare values can be assigned many bits.)

Example: Random Bit String

Consider a random sequence of 1s and 0s, i.e., the probability of a 0 or 1 is always $ P(0)=P(1)=1/2$ . The corresponding probability density function is

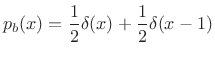$\displaystyle p_b(x) = \frac{1}{2}\delta(x) + \frac{1}{2}\delta(x-1)$ (D.31)

and the entropy is

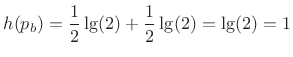$\displaystyle h(p_b) = \frac{1}{2}\lg(2) + \frac{1}{2}\lg(2) = \lg(2) = 1$ (D.32)

Thus, 1 bit is required for each bit of the sequence. In other words, the sequence cannot be compressed. There is no redundancy.

If instead the probability of a 0 is 1/4 and that of a 1 is 3/4, we get

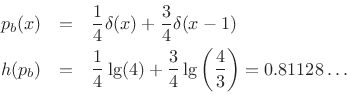
\begin{eqnarray*} p_b(x) &=& \frac{1}{4}\delta(x) + \frac{3}{4}\delta(x-1)\\ h(p_b) &=& \frac{1}{4}\lg(4) + \frac{3}{4}\lg\left(\frac{4}{3}\right) = 0.81128\ldots \end{eqnarray*}

and the sequence can be compressed about $ 19\%$ .

In the degenerate case for which the probability of a 0 is 0 and that of a 1 is 1, we get

\begin{eqnarray*} p_b(x) &=& \lim_{\epsilon \to0}\left[\epsilon \delta(x) + (1-\epsilon )\delta(x-1)\right]\\ h(p_b) &=& \lim_{\epsilon \to0}\epsilon \cdot\lg\left(\frac{1}{\epsilon }\right) + 1\cdot\lg(1) = 0. \end{eqnarray*}

Thus, the entropy is 0 when the sequence is perfectly predictable.

Maximum Entropy Distributions

Uniform Distribution

Among probability distributions $ p(x)$ which are nonzero over a finite range of values $ x\in[a,b]$ , the maximum-entropy distribution is the uniform distribution. To show this, we must maximize the entropy,

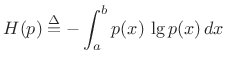$\displaystyle H(p) \isdef -\int_a^b p(x)\, \lg p(x)\, dx$ (D.33)

with respect to $ p(x)$ , subject to the constraints

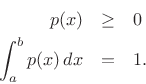
\begin{eqnarray*} p(x) &\geq& 0\\ \int_a^b p(x)\,dx &=& 1. \end{eqnarray*}

Using the method of Lagrange multipliers for optimization in the presence of constraints [86], we may form the objective function

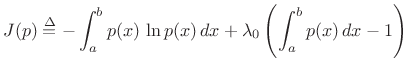$\displaystyle J(p) \isdef -\int_a^b p(x) \, \ln p(x) \,dx + \lambda_0\left(\int_a^b p(x)\,dx - 1\right)$ (D.34)

and differentiate with respect to $ p(x)$ (and renormalize by dropping the $ dx$ factor multiplying all terms) to obtain

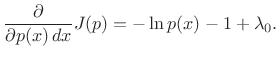$\displaystyle \frac{\partial}{\partial p(x)\,dx} J(p) = - \ln p(x) - 1 + \lambda_0.$ (D.35)

Setting this to zero and solving for $ p(x)$ gives

$\displaystyle p(x) = e^{\lambda_0-1}.$ (D.36)

(Setting the partial derivative with respect to $ \lambda_0$ to zero merely restates the constraint.)

Choosing $ \lambda_0$ to satisfy the constraint gives $ \lambda_0 =1-\ln(b-a)$ , yielding

$\displaystyle p(x) = \left\{\begin{array}{ll} \frac{1}{b-a}, & a\leq x \leq b \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right.$ (D.37)

That this solution is a maximum rather than a minimum or inflection point can be verified by ensuring the sign of the second partial derivative is negative for all $ x$ :

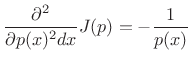$\displaystyle \frac{\partial^2}{\partial p(x)^2dx} J(p) = - \frac{1}{p(x)}$ (D.38)

Since the solution spontaneously satisfied $ p(x)>0$ , it is a maximum.

Exponential Distribution

Among probability distributions $ p(x)$ which are nonzero over a semi-infinite range of values $ x\in[0,\infty]$ and having a finite mean $ \mu$ , the exponential distribution has maximum entropy.

To the previous case, we add the new constraint

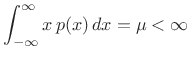$\displaystyle \int_{-\infty}^\infty x\,p(x)\,dx = \mu < \infty$ (D.39)

resulting in the objective function

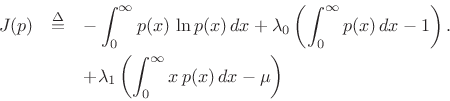
\begin{eqnarray*} J(p) &\isdef & -\int_0^\infty p(x) \, \ln p(x)\,dx + \lambda_0\left(\int_0^\infty p(x)\,dx - 1\right).\\ & & + \lambda_1\left(\int_0^\infty x\,p(x)\,dx - \mu\right) \end{eqnarray*}

Now the partials with respect to $ p(x)$ are

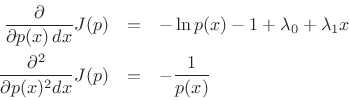
\begin{eqnarray*} \frac{\partial}{\partial p(x)\,dx} J(p) &=& - \ln p(x) - 1 + \lambda_0 + \lambda_1 x\\ \frac{\partial^2}{\partial p(x)^2 dx} J(p) &=& - \frac{1}{p(x)} \end{eqnarray*}

and $ p(x)$ is of the form $ p(x) = e^{(\lambda_0-1)+\lambda_1x}$ . The unit-area and finite-mean constraints result in $ \exp(\lambda_0-1) = 1/\mu$ and $ \lambda_1=-1/\mu$ , yielding

$\displaystyle p(x) = \left\{\begin{array}{ll} \frac{1}{\mu} e^{-x/\mu}, & x\geq 0 \\ [5pt] 0, & \hbox{otherwise}. \\ \end{array} \right.$ (D.40)

Gaussian Distribution

The Gaussian distribution has maximum entropy relative to all probability distributions covering the entire real line $ x\in(-\infty,\infty)$ but having a finite mean $ \mu$ and finite variance $ \sigma^2$ .

Proceeding as before, we obtain the objective function

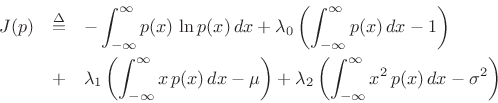
\begin{eqnarray*} J(p) &\isdef & -\int_{-\infty}^\infty p(x) \, \ln p(x)\,dx + \lambda_0\left(\int_{-\infty}^\infty p(x)\,dx - 1\right)\\ &+& \lambda_1\left(\int_{-\infty}^\infty x\,p(x)\,dx - \mu\right) + \lambda_2\left(\int_{-\infty}^\infty x^2\,p(x)\,dx - \sigma^2\right) \end{eqnarray*}

and partial derivatives

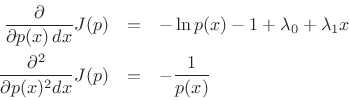
\begin{eqnarray*} \frac{\partial}{\partial p(x)\,dx} J(p) &=& - \ln p(x) - 1 + \lambda_0 + \lambda_1 x\\ \frac{\partial^2}{\partial p(x)^2 dx} J(p) &=& - \frac{1}{p(x)} \end{eqnarray*}

leading to

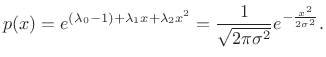$\displaystyle p(x) = e^{(\lambda_0-1)+\lambda_1 x + \lambda_2 x^2} = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{x^2}{2\sigma^2}}.$ (D.41)

For more on entropy and maximum-entropy distributions, see [48].

Gaussian Moments

Gaussian Mean

The mean of a distribution $ f(t)$ is defined as its first-order moment:

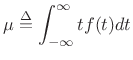$\displaystyle \mu \isdef \int_{-\infty}^\infty t f(t)dt$ (D.42)

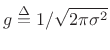To show that the mean of the Gaussian distribution is $ \mu$ , we may write, letting $ g\isdef 1/\sqrt{2\pi\sigma^2}$ ,

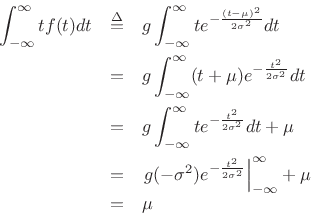
\begin{eqnarray*} \int_{-\infty}^\infty t f(t) dt &\isdef & g \int_{-\infty}^\infty t e^{-\frac{(t-\mu)^2}{2\sigma^2}} dt\\ &=&g \int_{-\infty}^\infty (t+\mu) e^{-\frac{t^2}{2\sigma^2}} dt\\ &=&g \int_{-\infty}^\infty t e^{-\frac{t^2}{2\sigma^2}} dt + \mu\\ &=&\left.g(-\sigma^2) e^{-\frac{t^2}{2\sigma^2}} \right\vert _{-\infty}^{\infty} + \mu\\ &=& \mu \end{eqnarray*}

since $ f(\pm\infty)=0$ .

Gaussian Variance

The variance of a distribution $ f(t)$ is defined as its second central moment:

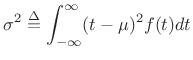$\displaystyle \sigma^2 \isdef \int_{-\infty}^\infty (t-\mu)^2 f(t)dt$ (D.43)

where $ \mu$ is the mean of $ f(t)$ .

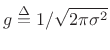To show that the variance of the Gaussian distribution is $ \sigma^2$ , we write, letting $ g\isdef 1/\sqrt{2\pi\sigma^2}$ ,

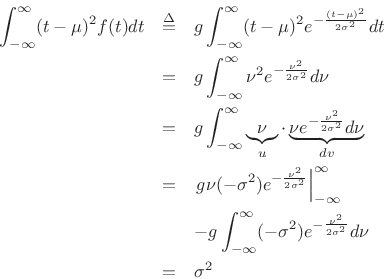
\begin{eqnarray*} \int_{-\infty}^\infty (t-\mu)^2 f(t) dt &\isdef & g \int_{-\infty}^\infty (t-\mu)^2 e^{-\frac{(t-\mu)^2}{2\sigma^2}} dt\\ &=&g \int_{-\infty}^\infty \nu^2 e^{-\frac{\nu^2}{2\sigma^2}} d\nu\\ &=&g \int_{-\infty}^\infty \underbrace{\nu}_{u} \cdot \underbrace{\nu e^{-\frac{\nu^2}{2\sigma^2}} d\nu}_{dv}\\ &=& \left. g \nu (-\sigma^2)e^{-\frac{\nu^2}{2\sigma^2}} \right\vert _{-\infty}^{\infty} \\ & & - g \int_{-\infty}^\infty (-\sigma^2) e^{-\frac{\nu^2}{2\sigma^2}} d\nu \\ &=&\sigma^2 \end{eqnarray*}

where we used integration by parts and the fact that $ \nu f(\nu)\to 0$ as $ \left\vert\nu\right\vert\to\infty$ .

Higher Order Moments Revisited


Theorem: The $ n$ th central moment of the Gaussian pdf $ p(x)$ with mean $ \mu$ and variance $ \sigma^2$ is given by

$\displaystyle m_n \isdef {\cal E}_p\{(x-\mu)^n\} = \left\{\begin{array}{ll} (n-1)!!\cdot\sigma^n, & \hbox{$n$\ even} \\ [5pt] $0$, & \hbox{$n$\ odd} \\ \end{array} \right. \protect$ (D.44)

where $ (n-1)!!$ denotes the product of all odd integers up to and including $ n-1$ (see ``double-factorial notation''). Thus, for example, $ m_2=\sigma^2$ , $ m_4=3\,\sigma^4$ , $ m_6=15\,\sigma^6$ , and $ m_8=105\,\sigma^8$ .


Proof: The formula can be derived by successively differentiating the moment-generating function $ M(\alpha) = {\cal E}_p\{\exp(\alpha x)\} = \exp(\mu \alpha + \sigma^2 \alpha^2 / 2)$ with respect to $ \alpha $ and evaluating at $ \alpha=0$ ,D.4 or by differentiating the Gaussian integral

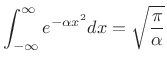$\displaystyle \int_{-\infty}^\infty e^{-\alpha x^2} dx = \sqrt{\frac{\pi}{\alpha}}$ (D.45)

successively with respect to $ \alpha $ [203, p. 147-148]:

\begin{eqnarray*} \int_{-\infty}^\infty (-x^2) e^{-\alpha x^2} dx &=& \sqrt{\pi}(-1/2)\alpha^{-3/2}\\ \int_{-\infty}^\infty (-x^2)(-x^2) e^{-\alpha x^2} + dx &=& \sqrt{\pi}(-1/2)(-3/2)\alpha^{-5/2}\\ \vdots & & \vdots\\ \int_{-\infty}^\infty x^{2k} e^{-\alpha x^2} dx &=& \sqrt{\pi}\,[(2k-1)!!]\,2^{-k/2}\alpha^{-(k+1)/2} \end{eqnarray*}

for $ k=1,2,3,\ldots\,$ . Setting $ \alpha = 1/(2\sigma^2)$ and $ n=2k$ , and dividing both sides by $ \sigma\sqrt{2\pi}$ yields

$\displaystyle {\cal E}_p\{x^n\} \isdefs \frac{1}{\sigma\sqrt{2\pi}}\int_{-\infty}^\infty x^n e^{-\frac{x^2}{2\sigma^2}} dx \eqsp \zbox {\sigma^n \cdot (n-1)!!}$ (D.46)

for $ n=2,4,6,\ldots\,$ . Since the change of variable $ x = \tilde{x}-\mu$ has no affect on the result, (D.44) is also derived for $ \mu\ne0$ .

Moment Theorem


Theorem: For a random variable $ x$ ,

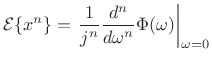$\displaystyle {\cal E}\{x^n\} = \left.\frac{1}{j^n}\frac{d^n}{d\omega^n}\Phi(\omega)\right\vert _{\omega=0}$ (D.47)

where $ \Phi(\omega)$ is the characteristic function of the PDF $ p(x)$ of $ x$ :

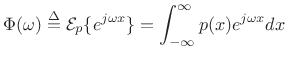$\displaystyle \Phi(\omega) \isdef {\cal E}_p\{ e^{j\omega x} \} = \int_{-\infty}^\infty p(x)e^{j\omega x}dx$ (D.48)

(Note that $ \Phi(\omega)$ is the complex conjugate of the Fourier transform of $ p(x)$ .)


Proof: [201, p. 157] Let $ m_i$ denote the $ i$ th moment of $ x$ , i.e.,

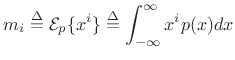$\displaystyle m_i \isdef {\cal E}_p\{x^i\} \isdef \int_{-\infty}^\infty x^i p(x)dx$ (D.49)

Then

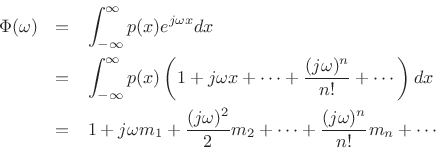
\begin{eqnarray*} \Phi(\omega) &=& \int_{-\infty}^\infty p(x)e^{j\omega x} dx \\ &=& \int_{-\infty}^\infty p(x) \left(1 + j\omega x + \cdots + \frac{(j\omega)^n}{n!}+\cdots\right)dx\\ &=& 1 + j\omega m_1 + \frac{(j\omega)^2}{2} m_2 + \cdots + \frac{(j\omega)^n}{n!}m_n+\cdots \end{eqnarray*}

where the term-by-term integration is valid when all moments $ m_i$ are finite.

Gaussian Characteristic Function

Since the Gaussian PDF is

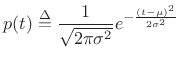$\displaystyle p(t) \isdef \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(t-\mu)^2}{2\sigma^2}}$ (D.50)

and since the Fourier transform of $ p(t)$ is

$\displaystyle P(\omega) = e^{-j\mu \omega} e^{-\frac{1}{2}\sigma^2\omega^2}$ (D.51)

It follows that the Gaussian characteristic function is

$\displaystyle \Phi(\omega) = \overline{P(\omega)} = e^{j\mu \omega} e^{-\frac{1}{2}\sigma^2\omega^2}.$ (D.52)

Gaussian Central Moments

The characteristic function of a zero-mean Gaussian is

$\displaystyle \Phi(\omega) = e^{-\frac{1}{2}\sigma^2\omega^2}$ (D.53)

Since a zero-mean Gaussian $ p(t)$ is an even function of $ t$ , (i.e., $ p(-t)=p(t)$ ), all odd-order moments $ m_i$ are zero. By the moment theorem, the even-order moments are

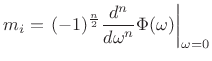$\displaystyle m_i = \left.(-1)^{\frac{n}{2}}\frac{d^n}{d\omega^n}\Phi(\omega)\right\vert _{\omega=0}$ (D.54)

In particular,

\begin{eqnarray*} \Phi^\prime(\omega) &=& -\frac{1}{2}\sigma^2 2\omega\Phi(\omega)\\ [5pt] \Phi^{\prime\prime}(\omega) &=& -\frac{1}{2}\sigma^2 2\omega\Phi^\prime(\omega) -\frac{1}{2}\sigma^2 2\Phi(\omega) \end{eqnarray*}

Since $ \Phi(0)=1$ and $ \Phi^\prime(0)=0$ , we see $ m_1=0$ , $ m_2=\sigma^2$ , as expected.

A Sum of Gaussian Random Variables is a Gaussian Random Variable

A basic result from the theory of random variables is that when you sum two independent random variables, you convolve their probability density functions (PDF). (Equivalently, in the frequency domain, their characteristic functions multiply.)

That the sum of two independent Gaussian random variables is Gaussian follows immediately from the fact that Gaussians are closed under multiplication (or convolution).

Next Section:
Bilinear Frequency-Warping for Audio Spectrum Analysis over Bark and ERB Frequency Scales
Previous Section:
Beginning Statistical Signal Processing