Fourier Transform of Complex Gaussian
Theorem:
 |
(D.16) |
Proof: [202, p. 211]
The Fourier transform of ![]() is defined as
is defined as
 |
(D.17) |
Completing the square of the exponent gives
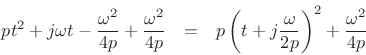
Thus, the Fourier transform can be written as
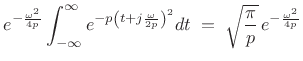 |
(D.18) |
using our previous result.
Alternate Proof
The Fourier transform of a complex Gaussian can also be derived using the differentiation theorem and its dual (§B.2).D.1
Proof: Let
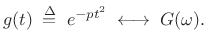 |
(D.19) |
Then by the differentiation theorem (§B.2),
| (D.20) |
By the differentiation theorem dual (§B.3),
| (D.21) |
Differentiating
![$\displaystyle g^\prime(t) \eqsp -2ptg(t) \eqsp \frac{2p}{j}[-jtg(t)] \;\longleftrightarrow\;\frac{2p}{j}G^\prime(\omega).$](http://www.dsprelated.com/josimages_new/sasp2/img2780.png) |
(D.22) |
Therefore,
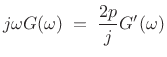 |
(D.23) |
or
![$\displaystyle \left[\ln G(\omega)\right]^\prime \eqsp \frac{G^\prime(\omega)}{G(\omega)} \eqsp -\frac{\omega}{2p} \eqsp \left(-\frac{\omega^2}{4p}\right)^\prime.$](http://www.dsprelated.com/josimages_new/sasp2/img2782.png) |
(D.24) |
Integrating both sides with respect to
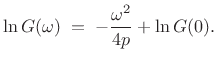 |
(D.25) |
In §D.7, we found that
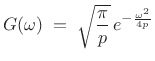 |
(D.26) |
as expected.
The Fourier transform of complex Gaussians (``chirplets'') is used in §10.6 to analyze Gaussian-windowed ``chirps'' in the frequency domain.
Next Section:
Why Gaussian?
Previous Section:
Gaussian Integral with Complex Offset



















