Constant-Overlap-Add (COLA) Cases

• Weak COLA: Window transform has zeros at frame-rate harmonics:
  
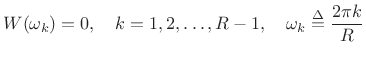
  • Perfect OLA reconstruction
  • Relies on aliasing cancellation in frequency domain
  • Aliasing cancellation is disturbed by spectral modifications
  • See Portnoff for further details
• Strong COLA: Window transform is bandlimited consistent with downsampling by the frame rate:
  
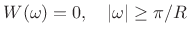
  • Perfect OLA reconstruction
  • No aliasing
  • better for spectral modifications
  • Time-domain window infinitely long in ideal case

Hamming Overlap-Add Example

Matlab code:

M = 33;         % window length
w = hamming(M);
R = (M-1)/2;    % maximum hop size
w(M) = 0;       % 'periodic Hamming' (for COLA)
%w(M) = w(M)/2; % another solution,
%w(1) = w(1)/2; %  interesting to compare

Figure 9.22: Periodic-Hamming OLA waveforms.

Periodic-Hamming OLA from Poisson Summation Formula

Matlab code:

ff = 1/R; % frame rate (fs=1)
N = 6*M;  % no. samples to look at OLA
sp = ones(N,1)*sum(w)/R; % dc term (COLA term)
ubound = sp(1);  % try easy-to-compute upper bound
lbound = ubound; % and lower bound
n = (0:N-1)';
for (k=1:R-1) % traverse frame-rate harmonics
  f=ff*k;
  csin = exp(j*2*pi*f*n); % frame-rate harmonic
  % find exact window transform at frequency f
  Wf = w' * conj(csin(1:M));
  hum = Wf*csin;   % contribution to OLA "hum"
  sp = sp + hum/R; % "Poisson summation" into OLA
  % Update lower and upper bounds:
  Wfb = abs(Wf);
  ubound = ubound + Wfb/R; % build upper bound
  lbound = lbound - Wfb/R; % build lower bound
end

In this example, the overlap-add is theoretically a perfect constant (equal to ) because the frame rate and all its harmonics coincide with nulls in the window transform (see Fig.9.24). A plot of the steady-state overlap-add and that computed using the Poisson Summation Formula (not shown) is constant to within numerical precision. The difference between the actual overlap-add and that computed using the PSF is shown in Fig.9.23. We verify that the difference is on the order of , which is close enough to zero in double-precision (64-bit) floating-point computations. We thus verify that the overlap-add of a length Hamming window using a hop size of samples is constant to within machine precision.

Figure 9.23: Periodic-Hamming Poisson summation formula test.

Figure 9.24 shows the zero-padded DFT of the modified Hamming window we're using ( ) with the frame-rate harmonics marked. In this example ( ), the upper half of the main lobe aliases into the lower half of the main lobe. (In fact, all energy above the folding frequency aliases into the lower half of the main lobe.) While this window and hop size still give perfect reconstruction under the STFT, spectral modifications will disturb the aliasing cancellation during reconstruction. This ``undersampled'' configuration is suitable as a basis for compression applications.

Figure 9.24: Hamming window transform and frame-rate.

Note that if we were to cut in half to , then the folding frequency in Fig.9.24 would coincide with the first null in the window transform. Since the frame rate and all its harmonics continue to land on nulls in the window transform, overlap-add is still exact. At this reduced hop size, however, the STFT becomes much more robust to spectral modifications, because all aliasing in the effective downsampled filter bank is now weighted by the side lobes of the window transform, with no aliasing components coming from within the main lobe. This is the central result of [9].

Kaiser Overlap-Add Example

M = 33;    % Window length
beta = 8;
w = kaiser(M,beta);
R = floor(1.7*(M-1)/(beta+1)); % ROUGH estimate (gives R=6)

Figure 9.25 plots the overlap-added Kaiser windows, and Fig.9.26 shows the steady-state overlap-add (a time segment sometime after the first 30 samples). The ``predicted'' OLA is computed using the Poisson Summation Formula using the same matlab code as before. Note that the Poisson summation formula gives exact results to within numerical precision. The upper (lower) bound was computed by summing (subtracting) the window-transform magnitudes at all frame-rate harmonics to (from) the dc gain of the window. This is one example of how the PSF can be used to estimate upper and lower bounds on OLA error.

Figure 9.25: Kaiser OLA waveforms.

Figure 9.26: Kaiser OLA, steady state.

The difference between measured steady-state overlap-add and that computed using the Poisson summation formula is shown in Fig.9.27. Again the two methods agree to within numerical precision.

Figure 9.27: Kaiser OLA from Poisson summation formula minus computed OLA.

Finally, Fig.9.28 shows the Kaiser window transform, with marks indicating the folding frequency at the chosen hop size , as well as the frame-rate and twice the frame rate. We see that the frame rate (hop size) has been well chosen for this window, as the folding frequency lies very close to what would be called the ``stop band'' of the Kaiser window transform. The ``stop-band rejection'' can be seen to be approximately dB (height of highest side lobe in Fig.9.28). We conclude that this example--a length 33 Kaiser window with and hop-size -- represents a reasonably high-quality audio STFT that will be robust in the presence of spectral modifications. We expect such robustness whenever the folding frequency lies above the main lobe of the window transform.

Figure 9.28: Kaiser window transform and frame-rate.

Remember that, for robustness in the presence of spectral modifications, the frame rate should be more than twice the highest main-lobe frequency.

Sign in