DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

FBS Fixed Modifications

Consider applying a fixed (time-invariant) filter $ H(\omega_k)$ to each $ X_m(\omega_k)$ before resynthesizing the signal:

$\displaystyle Y_m(\omega_k) = X_m(\omega_k)H(\omega_k)$ (10.28)

where, $ H(\omega_k)$ is the sampled frequency response of a filter with impulse response

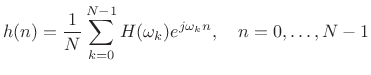$\displaystyle h(n) = \frac{1}{N} \sum_{k=0}^{N-1} H(\omega_k) e^{j\omega_kn}, \quad n=0,\ldots,N-1$ (10.29)

Let's examine the result this has on the signal in the time domain:

\begin{eqnarray*} y(m) &=& \frac{1}{N} \sum_{k=0}^{N-1} Y_m(\omega_k) e^{j\omega_k m} \\ &=& \frac{1}{N} \sum_{k=0}^{N-1} X_m(\omega_k)H(\omega_k) e^{j\omega_k m} \\ &=& \frac{1}{N} \sum_{k=0}^{N-1} \left\{ \sum_{n=-\infty}^\infty x(n)w(n-m)e^{-j\omega_kn} \right\} H(\omega_k) e^{j\omega_k m} \\ &=& \frac{1}{N} \sum_{n=-\infty}^\infty x(n)w(n-m) \sum_{k=0}^{N-1} H(\omega_k) e^{j\omega_k(m-n)} \\ &=& \sum_{n=-\infty}^\infty x(n) [ w(n-m) h(m-n)] \\ &=& \sum_{n=-\infty}^\infty x(n) [\tilde{w}(m-n)h(m-n)] \\ &=& (x*[\tilde{w} \cdot h])(m) \\ \end{eqnarray*}

We see that the result is $ x$ convolved with a windowed version of the impulse response $ h$ . This is in contrast to the OLA technique where the result gave us a windowed $ x$ filtered by $ h$ without the window having any effect on the filter, provided it obeys the COLA constraint and sufficient zero padding is used to avoid time aliasing.

In other words, FBS gives

$\displaystyle y = x * [\tilde{w} \cdot h] \;\longleftrightarrow\;X \cdot [{\tilde W}\ast H]$ (10.30)

while OLA gives (for $ R=1$ )

$\displaystyle y = x * [W(0)\cdot h] \;\longleftrightarrow\;X \cdot [W(0)\cdot H]$ (10.31)

  • In FBS, the analysis window 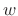$ w$ smooths the filter frequency response by time-limiting the corresponding impulse response.

  • In OLA, the analysis window can only affect scaling.

For these reasons, FFT implementations of FIR filters normally use the Overlap-Add method.

Next Section:
Time Varying Modifications in FBS
Previous Section:
Constant-Overlap-Add (COLA) Cases