Daniel Bernoulli's Modal Decomposition
The history of spectral modeling of sound arguably begins with Daniel Bernoulli, who first believed (in the 1733-1742 time frame) that any acoustic vibration could be expressed as a superposition of ``simple modes'' (sinusoidal vibrations) [52].G.1Bernoulli was able to show this precisely for the case of identical masses interconnected by springs to form a discrete approximation to an ideal string. Leonard Euler first wrote down (1749) a mathematical expression of Bernoulli's insight for a special case of the continuous vibrating string:
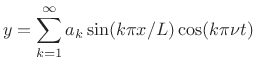 |
(G.1) |
Euler's paper was primarily in response to d'Alembert's landmark derivation (1747) of the traveling-wave picture of vibrating strings [266], which showed that vibrating string motion could assume essentially any twice-differentiable shape. Euler did not consider Bernoulli's sinusoidal superposition to be mathematically complete because clearly a trigonometric sum could not represent an arbitrary string shape.G.2D'Alembert did not believe that a superposition of sinusoids could be ``physical'' in part because he imagined what we would now call ``intermodulation distortion'' due to a high-frequency component ``riding on'' a lower-frequency component (as happens nowadays in loudspeakers).G.3 Arguments over the generality of the sinusoidal expansion of string vibration persisted for decades, embroiling also Lagrange, and were not fully settled until Fourier theory itself was wrestled into submission by the development of distribution theory, measure theory, and the notion of convergence ``almost everywhere.''
Note that organ builders had already for centuries built machines for performing a kind of ``additive synthesis'' by gating various ranks of pipes using ``stops'' as in pipe organs found today. However, the waveforms mixed together were not sinusoids, and were not regarded as mixtures of sinusoids. Theories of sound at that time, based on the ideas of Galileo, Mersenne, and Sauveur, et al. [52], were based on time-domain pulse-train analysis. That is, an elementary tone at a fixed pitch (and fundamental frequency) was a periodic pulse train, with the pulse-shape being non-critical. Musical consonance was associated with pulse-train coincidence--not frequency-domain separation. Bernoulli clearly suspected the spectrum analysis function integral to hearing as well as color perception [52, p. 359], but the concept of the ear as a spectrum analyzer is generally attributed to Helmholtz (1863) [293].
Next Section:
The Telharmonium
Previous Section:
Fundamental Frequency Estimation



















