Differentiation Theorem Dual
Theorem: Let 
denote a signal with Fourier transform 
, and let
 |
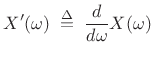(B.6) |
denote the derivative of
with respect to 
.
Then we have
 |
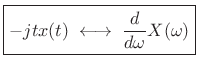(B.7) |
where
denotes the Fourier transform of 
.
Proof:
We can show this by direct differentiation of the definition of the
Fourier transform:
![\begin{eqnarray*}
X^\prime(\omega) &\isdef & \frac{d}{d\omega} \int_{-\infty}^{\infty} x(t) e^{-j\omega t} dt\\
&=& \int_{-\infty}^{\infty} x(t) (-jt) e^{-j\omega t} dt\\
&=& \int_{-\infty}^{\infty} [-jtx(t)] e^{-j\omega t} dt\\
&=& \hbox{\sc FT}_\omega\{[-jtx(t)]\}
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2429.png)
An alternate method of proof is given in §2.3.13.
The transform-pair may be alternately stated as follows:
 |
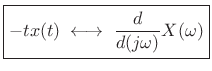(B.8) |
Next Section:
Scaling Theorem
Previous Section:
Differentiation Theorem
