DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Scaling Theorem

The scaling theorem (or similarity theorem) provides that if you horizontally ``stretch'' a signal by the factor $ \alpha $ in the time domain, you ``squeeze'' and amplify its Fourier transform by the same factor in the frequency domain. This is an important general Fourier duality relationship.


Theorem: For all continuous-time functions $ x(t)$ possessing a Fourier transform,

$\displaystyle \zbox {\hbox{\sc Stretch}_\alpha(x) \;\longleftrightarrow\;\left\vert\alpha\right\vert\hbox{\sc Stretch}_{(1/\alpha)}(X)} $ (B.9)

where

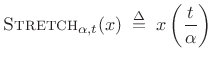$\displaystyle \hbox{\sc Stretch}_{\alpha,t}(x) \isdefs x\left(\frac{t}{\alpha}\right) $ (B.10)

and $ \alpha $ is any nonzero real number (the abscissa stretch factor). A more commonly used notation is the following:

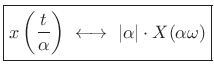$\displaystyle \zbox {x\left(\frac{t}{\alpha}\right) \;\longleftrightarrow\; \left\vert\alpha\right\vert\cdot X(\alpha\omega)}$ (B.11)


Proof: Taking the Fourier transform of the stretched signal gives

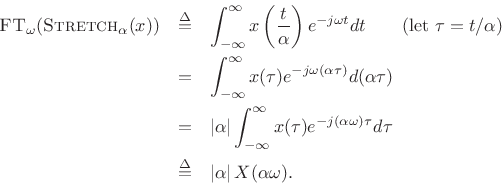
\begin{eqnarray*} \hbox{\sc FT}_{\omega}(\hbox{\sc Stretch}_\alpha(x)) &\isdef & \int_{-\infty}^\infty x\left(\frac{t}{\alpha}\right) e^{-j\omega t} dt\qquad\hbox{(let $\tau=t/\alpha$)}\\ &=& \int_{-\infty}^\infty x(\tau) e^{-j\omega (\alpha\tau)} d (\alpha\tau) \\ &=& \left\vert\alpha\right\vert\int_{-\infty}^\infty x(\tau) e^{-j(\alpha\omega)\tau} d \tau \\ &\isdef & \left\vert\alpha\right\vert X(\alpha\omega). \end{eqnarray*}

The absolute value appears above because, when $ \alpha<0$ , $ d (\alpha\tau) < 0$ , which brings out a minus sign in front of the integral from $ -\infty$ to $ \infty$ .

Next Section:
Shift Theorem
Previous Section:
Differentiation Theorem Dual