Flip Theorems
Let the flip operator be denoted by
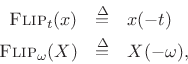
where
denotes time in seconds, and
denotes frequency in radians per second.
The following Fourier pairs are easily verified:
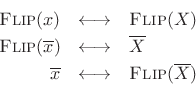
The proof of the first relation is as follows:
![\begin{eqnarray*}
\hbox{\sc FT}_{\omega}\left[\hbox{\sc Flip}(x)\right] &\isdef & \ensuremath{\int_{-\infty}^{\infty}}x(-t) e^{-j\omega t} dt\quad
\mbox{(set $\tau=-t$)}\\
&=& \int_{\infty}^{-\infty} x(\tau) e^{-j\omega (-\tau)} (-d\tau)\\
&=& \ensuremath{\int_{-\infty}^{\infty}}x(\tau) e^{-j(-\omega) \tau} d\tau\\
&=& X(-\omega) \isdef \hbox{\sc Flip}_\omega(X)
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2451.png)
Next Section:
Power Theorem
Previous Section:
Convolution Theorem
