DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Power Theorem

The power theorem for Fourier transforms states that the inner product of two signals in the time domain equals their inner product in the frequency domain.

The inner product of two spectra $ X(\omega)$ and $ Y(\omega)$ may be defined as

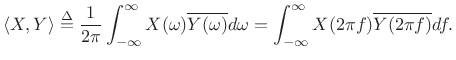$\displaystyle \left<X,Y\right> \isdef \frac{1}{2\pi} \ensuremath{\int_{-\infty}^{\infty}}X(\omega)\overline{Y(\omega)}d\omega = \ensuremath{\int_{-\infty}^{\infty}}X(2\pi f)\overline{Y(2\pi f)}df.$ (B.21)

This expression can be interpreted as the inverse Fourier transform of $ X\cdot\overline{Y}$ evaluated at $ t=0$ :

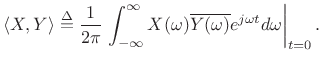$\displaystyle \left<X,Y\right> \isdef \frac{1}{2\pi} \left.\ensuremath{\int_{-\infty}^{\infty}}X(\omega)\overline{Y(\omega)}e^{j\omega t}d\omega\right\vert _{t=0}.$ (B.22)

By the convolution theorem (§B.7) and flip theorem (§B.8),

$\displaystyle X\cdot \overline{Y}\;\longleftrightarrow\;x\ast \hbox{\sc Flip}(\overline{y}),$ (B.23)

which at $ t=0$ gives

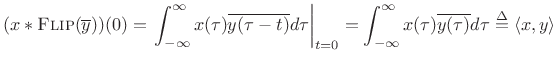$\displaystyle (x\ast \hbox{\sc Flip}(\overline{y}))(0) = \left.\ensuremath{\int_{-\infty}^{\infty}}x(\tau)\overline{y(\tau-t)}d\tau\right\vert _{t=0} = \ensuremath{\int_{-\infty}^{\infty}}x(\tau)\overline{y(\tau)}d\tau \isdef \left<x,y\right>$ (B.24)

Thus,

$\displaystyle \zbox {\left<x,y\right> \;\longleftrightarrow\;\left<X,Y\right>.}$ (B.25)

Next Section:
The Continuous-Time Impulse
Previous Section:
Flip Theorems