Convolution Theorem
The convolution theorem for Fourier transforms states that
convolution in the time domain equals multiplication in the
frequency domain. The continuous-time
convolution of two signals
and 
is defined by
 |
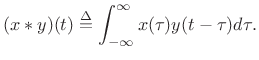(B.15) |
The Fourier transform is then
![\begin{eqnarray*}
\hbox{\sc FT}_\omega(x\ast y) &\isdef &
\int_{-\infty}^\infty
\left[\ensuremath{\int_{-\infty}^{\infty}}x(\tau)y(t-\tau)d\tau\right]
e^{-j\omega t}dt\\
&=&
\int_{-\infty}^\infty d\tau\, x(\tau)
\ensuremath{\int_{-\infty}^{\infty}}dt\, y(t-\tau)e^{-j\omega t}\\
&=&
\int_{-\infty}^\infty d\tau\, x(\tau) e^{-j\omega\tau}Y(\omega)
\quad\mbox{(by the \emph{shift theorem})}\\
&=& X(\omega)Y(\omega),
\end{eqnarray*}](http://www.dsprelated.com/josimages_new/sasp2/img2442.png)
or,
 |
(B.16) |
Exercise: Show that
 |
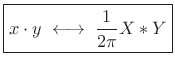(B.17) |
when frequency-domain convolution is defined by
 |
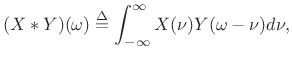(B.18) |
whereis in radians per second, and that
 |
(B.19) |
when frequency-domain convolution is defined by
 |
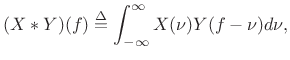(B.20) |
with
Next Section:
Flip Theorems
Previous Section:
Modulation Theorem (Shift Theorem Dual)
