Free Books
   Free Books    Spectral Audio Signal Processing  

Gaussian Integral with Complex Offset


Theorem:

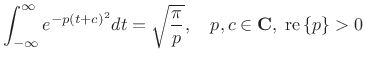$\displaystyle \int_{-\infty}^\infty e^{-p(t+c)^2}dt = \sqrt{\frac{\pi}{p}}, \quad p,c\in {\bf C},\;\mbox{re}\left\{p\right\}>0$ (D.12)


Proof: When $ c=0$ , we have the previously proved case. For arbitrary $ c=a+jb\in{\bf C}$ and real number $ T>\left\vert a\right\vert$ , let $ \Gamma_c(T)$ denote the closed rectangular contour $ z = (-T) \to T \to (T+jb) \to (-T+jb) \to (-T)$ , depicted in Fig.D.1.

Figure D.1: Contour of integration in the complex plane.
\includegraphics[width=0.8\twidth]{eps/gammarect}

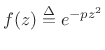Clearly, $ f(z) \isdef e^{-pz^2}$ is analytic inside the region bounded by $ \Gamma_c(T)$ . By Cauchy's theorem [42], the line integral of $ f(z)$ along $ \Gamma_c(T)$ is zero, i.e.,

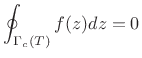$\displaystyle \oint_{\Gamma_c(T)} f(z) dz = 0$ (D.13)

This line integral breaks into the following four pieces:

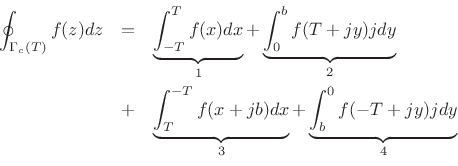
\begin{eqnarray*} \oint_{\Gamma_c(T)} f(z) dz &=& \underbrace{\int_{-T}^T f(x) dx}_1 + \underbrace{\int_{0}^{b} f(T+jy) jdy}_2\\ &+& \underbrace{\int_{T}^{-T} f(x+jb) dx}_3 + \underbrace{\int_{b}^{0} f(-T+jy) jdy}_4\\ \end{eqnarray*}

where $ x$ and $ y$ are real variables. In the limit as $ T\to\infty$ , the first piece approaches $ \sqrt{\pi/p}$ , as previously proved. Pieces $ 2$ and $ 4$ contribute zero in the limit, since $ e^{-p(t+c)^2} \to 0$ as $ \left\vert t\right\vert\to\infty$ . Since the total contour integral is zero by Cauchy's theorem, we conclude that piece 3 is the negative of piece 1, i.e., in the limit as $ T\to\infty$ ,

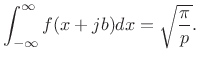$\displaystyle \int_{-\infty}^\infty f(x+jb) dx = \sqrt{\frac{\pi}{p}}.$ (D.14)

Making the change of variable $ x=t+a=t+c-jb$ , we obtain

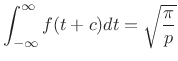$\displaystyle \int_{-\infty}^\infty f(t+c) dt = \sqrt{\frac{\pi}{p}}$ (D.15)

as desired.

Next Section:
Fourier Transform of Complex Gaussian
Previous Section:
Integral of a Complex Gaussian