Integral of a Complex Gaussian
Theorem:
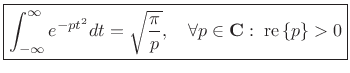 |
(D.7) |
Proof: Let ![]() denote the integral. Then
denote the integral. Then
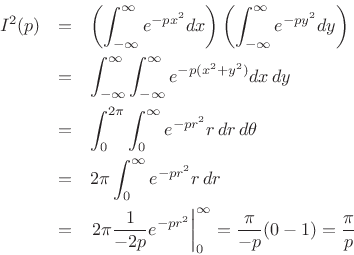
where we needed
re![]() to have
to have
![]() as
as
![]() . Thus,
. Thus,
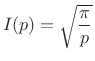 |
(D.8) |
as claimed.
Area Under a Real Gaussian
Corollary:
Setting
![]() in the previous theorem, where
in the previous theorem, where ![]() is real,
we have
is real,
we have
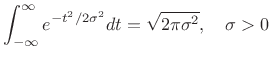 |
(D.9) |
Therefore, we may normalize the Gaussian to unit area by defining
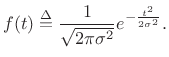 |
(D.10) |
Since
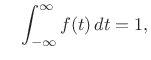 |
(D.11) |
it satisfies the requirements of a probability density function.
Next Section:
Gaussian Integral with Complex Offset
Previous Section:
Infinite Flatness at Infinity



















