Gaussians Closed under Multiplication

Free Books Spectral Audio Signal Processing

Define

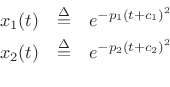
$\begin{eqnarray*} x_1(t) &\isdef & e^{-p_1(t+c_1)^2}\\ x_2(t) &\isdef & e^{-p_2(t+c_2)^2}\\ \end{eqnarray*}$

where are arbitrary complex numbers. Then by direct calculation, we have

$\begin{eqnarray*} x_1(t)\cdot x_2(t) &=& e^{-p_1(t+c_1)^2} e^{-p_2(t+c_2)^2}\\ &=& e^{-p_1 t^2 - 2 p_1 c_1 t - p_1 c_1^2 -p_2 t^2 - 2 p_2 c_2 t - p_2 c_2^2}\\ &=& e^{-(p_1+p_2) t^2 - 2 (p_1 c_1 + p_2 c_2) t - (p_1 c_1^2 + p_2 c_2^2)}\\ &=& e^{-(p_1+p_2)\left[t^2 + 2\frac{p_1 c_1 + p_2 c_2}{p_1 + p_2} t + \frac{p_1 c_1^2 + p_2 c_2^2}{p_1 + p_2}\right]} \end{eqnarray*}$

Completing the square, we obtain

$\displaystyle x_1(t)\cdot x_2(t) = g \cdot e^{-p(t+c)^2}$

(D.2)

with

$\begin{eqnarray*} p &=& p_1+p_2\\ [5pt] c &=& \frac{p_1 c_1 + p_2 c_2}{p_1 + p_2}\\ [5pt] g &=& e^{-p_1 p_2 \frac{(c_1 - c_2)^2}{p_1 + p_2}} \end{eqnarray*}$

Note that this result holds for Gaussian-windowed chirps ( and complex).

Product of Two Gaussian PDFs

For the special case of two Gaussian probability densities,

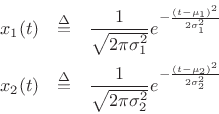
$\begin{eqnarray*} x_1(t) &\isdef & \frac{1}{\sqrt{2\pi\sigma_1^2}}e^{-\frac{(t-\mu_1)^2}{2\sigma_1^2}}\\ x_2(t) &\isdef & \frac{1}{\sqrt{2\pi\sigma_2^2}}e^{-\frac{(t-\mu_2)^2}{2\sigma_2^2}} \end{eqnarray*}$

the product density has mean and variance given by

$\begin{eqnarray*} \mu &=& \frac{\frac{\mu_1}{2\sigma_1^2} + \frac{\mu_2}{2\sigma_2^2}}{\frac{1}{2\sigma_1^2} + \frac{1}{2\sigma_2^2}} \;\eqsp \; \frac{\mu_1\sigma_2^2 + \mu_2\sigma_1^2}{\sigma_2^2 + \sigma_1^2}\\ [5pt] \sigma^2 &=& \left. \sigma_1^2 \right\Vert \sigma_2^2 \;\isdefs \; \frac{1}{\frac{1}{\sigma_1^2} + \frac{1}{\sigma_2^2}} \;\eqsp \; \frac{\sigma_1^2\sigma_2^2}{\sigma_1^2 + \sigma_2^2}. \end{eqnarray*}$

Next Section:
Gaussians Closed under Convolution
Previous Section:
Gaussian Window and Transform