Gaussian Window and Transform
The Gaussian window for FFT analysis was introduced in §3.11, and complex Gaussians (``chirplets'') were utilized in §10.6. For reference in support of these topics, this appendix derives some additional properties of the Gaussian, defined by
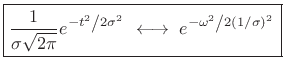 |
(D.1) |
and discusses some interesting applications in spectral modeling (the subject of §10.4). The basic mathematics rederived here are well known (see, e.g., [202,5]), while the application to spectral modeling of sound remains a topic under development.
Next Section:
Gaussians Closed under Multiplication
Previous Section:
White Noise



















