DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Haar Example

Before we leave the case of amplitude-complementary, two-channel, critically sampled, perfect reconstruction filter banks, let's see what happens when $ H_0(z)$ is the simplest possible lowpass filter having unity dc gain, i.e.,

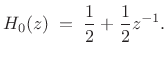$\displaystyle H_0(z) \eqsp \frac{1}{2} + \frac{1}{2}z^{-1}.$ (12.29)

This case is obtained above by setting $ E_0(z^2)=1/2$ , $ o=1$ , and $ h_0(1)=1/2$ . The polyphase components of $ H_0(z)$ are clearly

$\displaystyle E_0(z^2)\eqsp E_1(z^2)\eqsp 1/2.$ (12.30)

Choosing $ H_1(z)=1-H_0(z)$ , and choosing $ F_0(z)$ and $ F_1(z)$ for aliasing cancellation, the four filters become

\begin{eqnarray*} H_0(z) &=& \frac{1}{2} + \frac{1}{2}z^{-1} \eqsp E_0(z^2)+z^{-1}E_1(z^2)\\ [5pt] H_1(z) &=& 1-H_0(z) \eqsp \frac{1}{2} - \frac{1}{2}z^{-1} \eqsp E_0(z^2)-z^{-1}E_1(z^2)\\ [5pt] F_0(z) &=& \;\;\, H_1(-z) \eqsp \frac{1}{2} + \frac{1}{2}z^{-1} \eqsp \;\;\,H_0(z)\\ [5pt] F_1(z) &=& -H_0(-z) \eqsp -\frac{1}{2} + \frac{1}{2}z^{-1} \eqsp -H_1(z). \end{eqnarray*}

Thus, both the analysis and reconstruction filter banks are scalings of the familiar Haar filters (``sum and difference'' filters $ (1\pm z^{-1})/\sqrt{2}$ ). The frequency responses are

\begin{eqnarray*} H_0(e^{j\omega}) &=&\;\;\,F_0(e^{j\omega}) \eqsp \frac{1}{2} + \frac{1}{2}e^{-j\omega}\eqsp e^{-j\frac{\omega}{2}} \cos\left(\frac{\omega}{2}\right)\\ [5pt] H_1(e^{j\omega}) &=& -F_0(e^{j\omega}) \eqsp \frac{1}{2} - \frac{1}{2}e^{-j\omega}\eqsp j e^{-j\frac{\omega}{2}} \sin\left(\frac{\omega}{2}\right) \end{eqnarray*}

which are plotted in Fig.11.16.

Figure 11.16: Amplitude responses of the two channel filters in the Haar filter bank.
\includegraphics[width=\twidth]{eps/haar}

Next Section:
Polyphase Decomposition of Haar Example
Previous Section:
Amplitude-Complementary 2-Channel Filter Bank