DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Polyphase Decomposition of Haar Example


\begin{psfrags} % latex2html id marker 29979\psfrag{x(n)}{\normalsize $x(n)$}\psfrag{x}{\normalsize $x$}\psfrag{(n)}{\normalsize $(n)$}\psfrag{y}{\normalsize $y$}\psfrag{v}{\normalsize $v$}\psfrag{H}{\normalsize $H$}\psfrag{F}{\normalsize $F$}\psfrag{z}{\normalsize $z$}\begin{figure}[htbp] \includegraphics[width=\twidth]{eps/cqfcopy} \caption{Two-channel polyphase filter bank and inverse.} \end{figure} \end{psfrags}

Let's look at the polyphase representation for this example. Starting with the filter bank and its reconstruction (see Fig.11.17), the polyphase decomposition of $ H_0(z)$ is

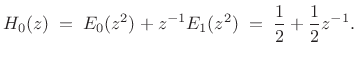$\displaystyle H_0(z) \eqsp E_0(z^2) + z^{-1}E_1(z^2) \eqsp \frac{1}{2}+\frac{1}{2}z^{-1}.$ (12.31)

Thus, $ E_0(z^2)=E_1(z^2)=1/2$ , and therefore

$\displaystyle H_1(z) \eqsp 1-H_0(z) \eqsp E_0(z^2)-z^{-1}E_1(z^2).$ (12.32)

We may derive polyphase synthesis filters as follows:

\begin{eqnarray*} \hat{X}(z) &=& \left[F_0(z)H_0(z) + F_1(z)H_1(z)\right] X(z)\\ &=& \left[\left(\frac{1}{2} + \frac{1}{2}z^{-1}\right)H_0(z) + \left(-\frac{1}{2}+\frac{1}{2}z^{-1}\right)H_1(z)\right]X(z)\\ &=& \frac{1}{2}\left\{\left[H_0(z)-H_1(z)\right] + z^{-1}\left[H_0(z) + H_1(z)\right]\right\}X(z) \end{eqnarray*}

The polyphase representation of the filter bank and its reconstruction can now be drawn as in Fig.11.18. Notice that the reconstruction filter bank is formally the transpose of the analysis filter bank [263]. A filter bank that is inverted by its own transpose is said to be an orthogonal filter bank, a subject to which we will return §11.3.8.

Figure 11.18: Polyphase representation of the general two-channel, critically sampled filter bank and its inverse.
\includegraphics[width=\twidth]{eps/poly2chan}

Figure 11.19: Figure 11.18 with downsamplers commuted inside the filter branches.
\includegraphics[width=\twidth]{eps/poly2chanfast}

Commuting the downsamplers (using the noble identities from §11.2.5), we obtain Figure 11.19. Since $ E_0(z)=E_1(z)=1/2$ , this is simply the OLA form of an STFT filter bank for $ N=2$ , with $ N=M=R=2$ , and rectangular window $ w=[1/2,1/2]$ . That is, the DFT size, window length, and hop size are all 2, and both the DFT and its inverse are simply sum-and-difference operations.


Next Section:
Quadrature Mirror Filters (QMF)
Previous Section:
Haar Example