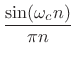The Ideal Lowpass Filter
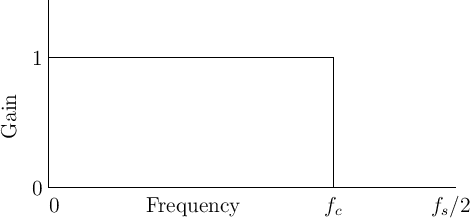
Consider the ideal lowpass filter, depicted in Fig.4.1.
An ideal lowpass may be characterized by a gain of 1 for all
frequencies below some cut-off frequency ![]() in Hz, and a
gain of 0 for all higher frequencies.5.2
The impulse response of the ideal lowpass filter
is easy to calculate:
in Hz, and a
gain of 0 for all higher frequencies.5.2
The impulse response of the ideal lowpass filter
is easy to calculate:
where
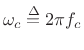 denotes the normalized cut-off
frequency in radians per sample. Thus, the impulse response of an
ideal lowpass filter is a sinc function.
denotes the normalized cut-off
frequency in radians per sample. Thus, the impulse response of an
ideal lowpass filter is a sinc function.
Unfortunately, we cannot implement the ideal lowpass filter in
practice because its impulse response is infinitely long in
time. It is also noncausal; it cannot be shifted to make it
causal because the impulse response extends all the way to time
![]() . It is clear we will have to accept some sort of
compromise in the design of any practical lowpass filter.
. It is clear we will have to accept some sort of
compromise in the design of any practical lowpass filter.
The subject of digital filter design is generally concerned with finding an optimal approximation to the desired frequency response by minimizing some norm of a prescribed error criterion with respect to a set of practical filter coefficients, perhaps subject also to some constraints (usually linear equality or inequality constraints) on the filter coefficients, as we saw for optimal window design in §3.13.5.3In audio applications, optimality is difficult to define precisely because perception is involved. It is therefore valuable to consider also suboptimal methods that are ``close enough'' to optimal, and which may have other advantages such as extreme simplicity and/or speed. We will examine some specific cases below.
Next Section:
Lowpass Filter Design Specifications
Previous Section:
Window Design by Linear Programming








![$\displaystyle \frac{1}{2\pi}\int_{-\pi}^{\pi} d\omega e^{j\omega n }
\left\{\begin{array}{ll}
1, & \left\vert\omega\right\vert\leq\omega_c \\ [5pt]
0, & \mbox{otherwise} \\
\end{array} \right.$](http://www.dsprelated.com/josimages_new/sasp2/img653.png)
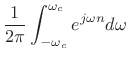
![$\displaystyle \frac{1}{2\pi jn}\left[e^{j\omega_c n} - e^{-j\omega_c n}\right]$](http://www.dsprelated.com/josimages_new/sasp2/img655.png)