Free Books
   Free Books    Spectral Audio Signal Processing  

Lowpass Filter Design Specifications

Typical design parameters for a lowpass filter are shown in Fig.4.2.

Figure 4.2: Illustration of typical lowpass filter specifications in the frequency domain.
\includegraphics[width=4in]{eps/idealFilter}

The design parameters are defined as follows:

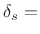  • $ \delta_s = $ stop-band ripple ( 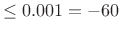$ \leq 0.001 = -60 $ dB is common)
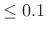  • $ \delta_p = $ pass-band ripple ($ \leq 0.1$ dB typical)
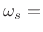  • $ \omega_s = $ stop-band edge frequency
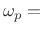  • $ \omega_p = $ pass-band edge frequency
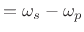
  • TW: transition width $ = \omega_s - \omega_p $
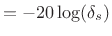
  • SBA: stop-band attenuation $ = -20 \log( \delta_s ) $
The pass-band ripple is typically larger than the stop-band ripple because it is a deviation about 1 instead of 0. For example, a pass-band ripple of $ \pm 0.1$ dB translates to $ 10^{0.1/20}-1 \approx 0.01$ on a linear scale. A stop-band ripple of $ -60$ dB, on the other hand, equals $ 10^{-60/20} = 0.001$ on a linear scale. Thus, a typical pass-band ripple specification may be 10 times larger than a typical stop-band ripple specification, on a linear scale, though less audible.5.4 For a stop-band gain down around $ -80$ dB, keeping the pass-band ripple at $ \pm 0.1$ dB, the pass-band ripple becomes around 100 times larger than the stop-band ripple, on a linear scale, but again the stop-band ripple is more likely to yield audible error in typical situations. In summary, the pass-band ripple is an allowed gain deviation, while the stop-band ripple is an allowed ``leakage'' level.

In terms of these specifications, we may define an optimal FIR lowpass filter of a given length to be one which minimizes the stop-band and pass-band ripple (weighted relatively as desired) for given stop-band and pass-band edge frequencies. Such optimal filters are often designed in practice by Chebyshev methods, as we encountered already in the study of windows for spectrum analysis (§3.10,§3.13). Optimal Chebyshev FIR filters will be discussed further below (in §4.5.2), but first we look at simpler FIR design methods and compare to optimal Chebyshev designs for reference. An advantage of the simpler methods is that they are more suitable for interactive, real-time, and/or signal-adaptive FIR filter design.

Ideal Lowpass Filter Revisited

The ideal lowpass filter of Fig.4.1 can now be described by the following specifications:

  • The transition width TW is zero ( 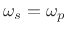$ \omega_s=\omega_p$ in Fig.4.2).
  • The pass-band and stop-band ripples are both zero
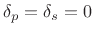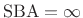    ( $ \delta_p = \delta_s = 0$ in Fig.4.2, and $ \hbox{SBA} = \infty$ ).
As discussed above, these specifications are not achievable by any FIR filter. It is instructive, however, to see how an optimal least-squares design comes out in this case.

Next Section:
Optimal (but poor if unweighted) Least-Squares Impulse Response Design
Previous Section:
The Ideal Lowpass Filter