Free Books
   Free Books    Spectral Audio Signal Processing  

Ideal Spectral Interpolation

Ideally, the spectrum of any signal $ x(n)$ at any frequency $ \omega = 2\pi f$ is obtained by projecting the signal $ x$ onto the zero-phase, unit-amplitude, complex sinusoid at frequency $ \omega$ [264]:

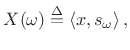$\displaystyle X(\omega) \isdef \left<x,s_\omega\right>,$ (3.43)

where

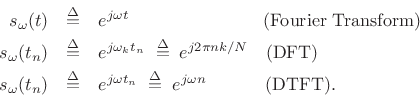
\begin{eqnarray*} s_\omega(t) &\isdef & e^{j\omega t}\qquad\qquad\qquad\quad\;\,\mbox{(Fourier Transform)}\\ s_\omega(t_n) &\isdef & e^{j\omega_k t_n} \isdefs e^{j2\pi nk/N} \quad\mbox{(DFT)} \\ s_\omega(t_n) &\isdef & e^{j\omega t_n} \isdefs e^{j\omega n} \quad\qquad\;\mbox{(DTFT)}. \end{eqnarray*}

Thus, for signals in the DTFT domain which are time limited to $ n\in[-N/2,N/2-1]$ , we obtain

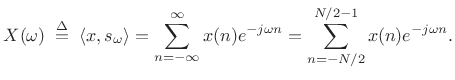$\displaystyle X(\omega) \isdefs \left<x,s_\omega\right> = \sum_{n=-\infty}^\infty x(n) e^{-j\omega n} = \sum_{n=-N/2}^{N/2-1} x(n) e^{-j\omega n}.$ (3.44)

This can be thought of as a zero-centered DFT evaluated at $ \omega\in[-\pi,\pi)$ instead of $ \omega_k = 2\pi k/N$ for some $ k\in[0,N-1]$ . It arises naturally from taking the DTFT of a finite-length signal. Such time-limited signals may be said to have ``finite support'' [175].

Next Section:
Interpolating a DFT
Previous Section:
Spectral Roll-Off