DSPRelated.com
Free Books
   Free Books    Spectral Audio Signal Processing  

Natural Basis

The natural basis for a discrete-time signal $ x(n)$ is the set of shifted impulses:

$\displaystyle \varphi_k \isdefs [\ldots, 0,\underbrace{1}_{k^{\hbox{\tiny th}}},0,\ldots],$ (12.108)

or,

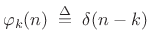$\displaystyle \varphi_k (n) \isdefs \delta(n-k)$ (12.109)

for all integers $ k$ and $ n$ . The basis set is orthonormal since $ \left<\varphi_k ,\varphi_l \right>=\delta(k-l)$ . The coefficient of projection of $ x$ onto $ \varphi_k $ is given by

$\displaystyle \left<\varphi_k ,x\right> \eqsp x(k)$ (12.110)

so that the expansion of $ x$ in terms of the natural basis is simply

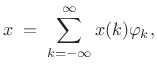$\displaystyle x \eqsp \sum_{k=-\infty}^{\infty}x(k) \varphi_k ,$ (12.111)

i.e.,
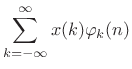$\displaystyle x(n)$ $\displaystyle =$ $\displaystyle \sum_{k=-\infty}^{\infty}x(k) \varphi_k (n)$  
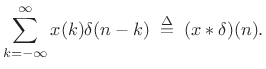  $\displaystyle =$ $\displaystyle \sum_{k=-\infty}^{\infty}x(k) \delta(n-k) \isdefs (x \ast \delta)(n).$  

This expansion was used in Book II [263] to derive the impulse-response representation of an arbitrary linear, time-invariant filter.

Next Section:
Normalized DFT Basis for
Previous Section:
Example: Upsampling by 2