Normalized DFT Basis for 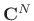| Spectral Audio Signal Processing

Normalized DFT Basis for ${\bf C}^N$

The Normalized Discrete Fourier Transform (NDFT) (introduced in Book I [264]) projects the signal onto discrete-time sinusoids of length , where the sinusoids are normalized to have unit norm:

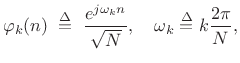$\displaystyle \varphi_k (n) \isdefs \frac{e^{j\omega_k n}}{\sqrt{N}}, \quad \omega_k \isdef k\frac{2\pi}{N},$

(12.112)

and $n,k \in [0,N-1]$ . The coefficient of projection of onto $\varphi_k$ is given by

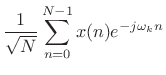$\displaystyle \left<\varphi_k ,x\right>$	$\displaystyle \isdef$	$\displaystyle \frac{1}{\sqrt{N}}\sum_{n=0}^{N-1} x(n) e^{-j\omega_k n}$
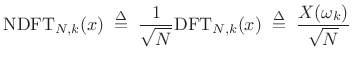	$\displaystyle \isdef$	$\displaystyle \hbox{NDFT}_{N,k}(x) \isdefs \frac{1}{\sqrt{N}}\hbox{DFT}_{N,k}(x) \isdefs \frac{X(\omega_k )}{\sqrt{N}}$

and the expansion of in terms of the NDFT basis set is

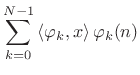$\displaystyle x(n)$	$\displaystyle =$	$\displaystyle \sum_{k=0}^{N-1} \left<\varphi_k ,x\right> \varphi_k (n)$
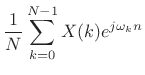	$\displaystyle =$	$\displaystyle \frac{1}{N} \sum_{k=0}^{N-1} X(k)e^{j\omega_k n}$
	$\displaystyle \isdef$	$\displaystyle \hbox{DFT}_{N,n}^{-1}(X)$